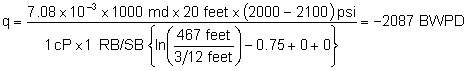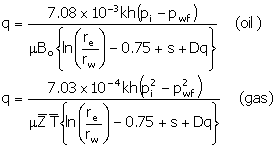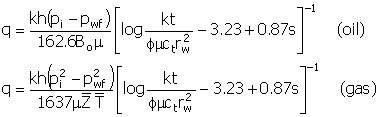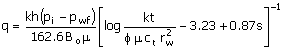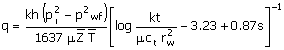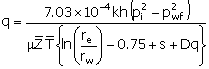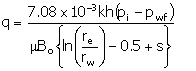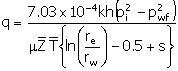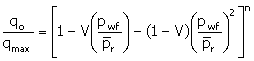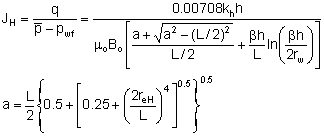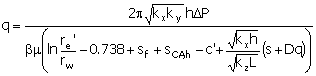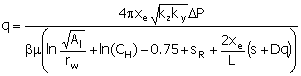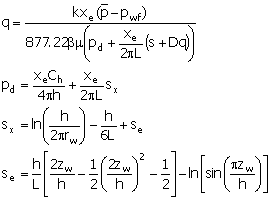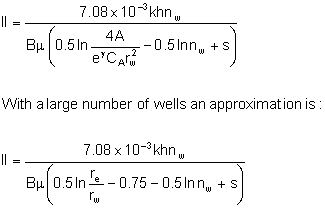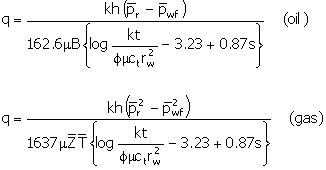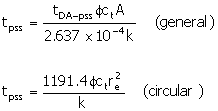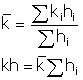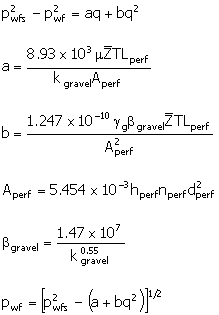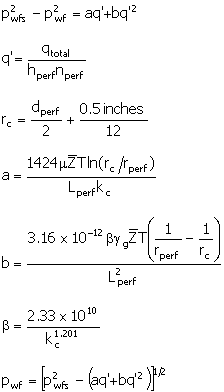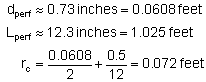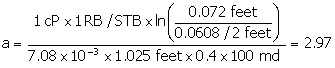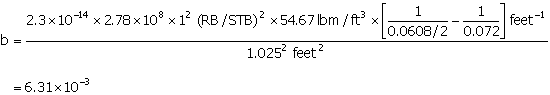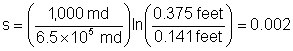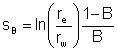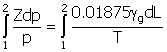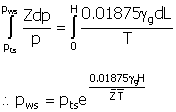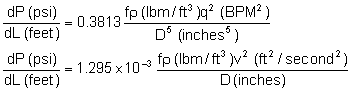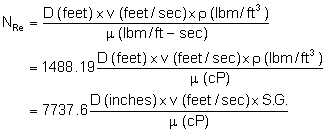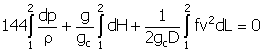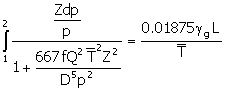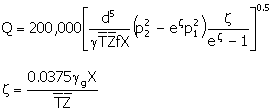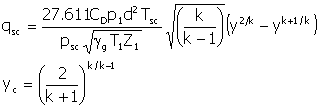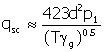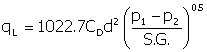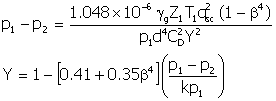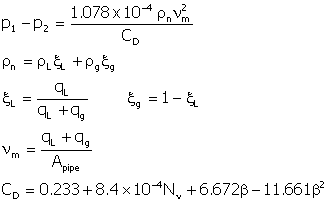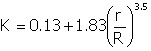Injection Performance Relationships – Single Phase
As you can see in the previous equations, pressure change in
the reservoir and injection are related by Darcy’s Law. The injection into a reservoir, as a
function of the reservoir parameters and the pressure differential can be
characterized over a range of pressure differences (difference between the
bottomhole pressure and the reservoir pressure). In its simplest form, this is
a straight line (assuming single phase flow and using Darcy’s Law for
steady-state conditions), until fracturing occurs, as shown in Figure 1.
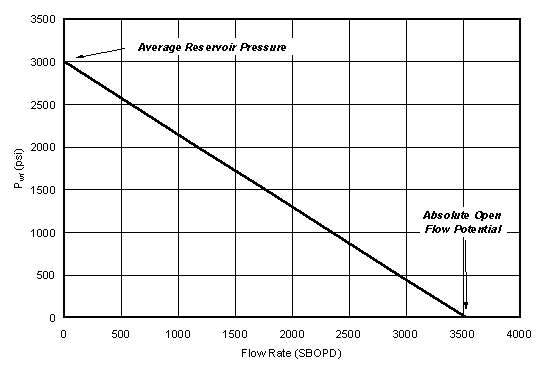
Figure 1. The
performance relationship for a characteristic well for single phase, laminar
flow of a slightly compressible liquid.
This example is for production.
Injection is analogous.
By assuming pseudo-steady-state or steady-state radial flow,
the performance curve for an injector above the bubble point (the pressure is
high enough that gas is in solution) can be developed from (same as Equation
1):
|
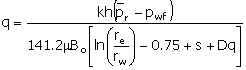
|
(5)
|
Figure 1 represents a well with water injection. Similar
relationships are available for gas.
The curve shown (Figures 1) does not reflect restrictions
imposed by the completion itself and any tubulars or damage/stimulation (skin).
These curves provide a starting point for determining the flow and pressure
conditions that you will encounter during your injection operations.
The Effect of Skin on Performance
You can see from the basic equations that performance
relationships are affected by skin – damage or flow restriction or flow
improvement. According to Earlougher, “There are several ways to quantify
damage or improvement in operating (producing or injecting) wells. A favored
method represents the wellbore condition by a steady-state pressure drop at the
wellface in addition to the normal pressure drop in the reservoir. The
additional pressure drop, called the “skin effect,” occurs in an
infinitesimally thin “skin zone” [for mathematical purposes even though damage
may extend deep into the formation]. In the flow equation …, the degree of
damage (or improvement) is expressed in terms of a “skin
factor" (s) which is positive for damage and negative for improvement. It
can vary from about –5 for a hydraulically fractured well to + ¥ for a well that is too badly damaged to
produce” (Earlougher, 1977).
The skin factor itself is dimensionless, but you can have an
indication of the supplementary pressure drop caused by skin (relative to an
undamaged well) for radial, non-turbulent liquid flow using:
|
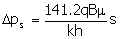
|
(6)
|
where:
|
Dps
|
=
|
pressure drop due to skin (psi)
|
It is important to consider the skin factor that the
completion will develop, how much skin can be alleviated by manipulating the
pressure during completion, and in the longer term, deciding when a well will
need to be worked over or abandoned. Alternatively to Equation 6, you can
calculate the skin by specifying a finite depth of damage in the formation
using:
|
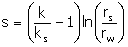
|
(7)
|
where:
|
ks
|
=
|
permeability of the damaged zone (md)
|
|
rs
|
=
|
radial extent of the damaged zone (feet)
|
Unfortunately, the depth of damage and the damaged zone
permeability are hard to infer. You can also assess the influence of skin by
considering skin in terms of an apparent (or effective) wellbore radius:
|
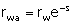
|
(8)
|
where:
rwa = apparent wellbore radius. Positive skin
implies that the well has been damaged and the apparent wellbore radius is
reduced, and vice versa for a stimulated well (feet).
This relationship implies a reduced apparent wellbore radius
(and consequently less production) for positive skin. Figure 2 shows skin schematically.
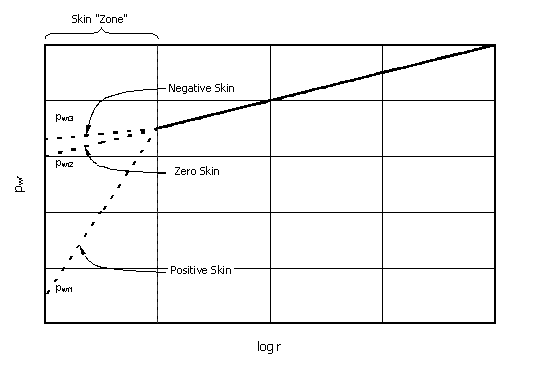
Figure 2. Schematic
representation of the variation of skin as a pressure drop through the
reservoir, for a particular flow rate. With positive skin more pressure is
required to achieve a particular rate.
Note that this shows the “real” variation of damage/improvement away
from the well. Some of the mathematical
treatments represent this pressure change as occurring in an infinitely thin
zone at the wellbore. This figure is
for production. Similar figures are
possible for injection.
Skin can develop in a number of
different ways, some depending on the damage done to the formation during
drilling and/or completion, some due to the completion itself, and some even
due strictly to the inclination of the well. The total skin is the combination
of mechanical and pseudo-skins (total skin is determined from well testing
analysis).
Mechanical skin is associated with formation damage due
to drilling fluids, cementing, etc. Mechanical skin is mathematically defined
as an infinitely thin zone that creates a steady-state pressure drop at the
formation face. A primary goal is to minimize turbulence, multiphase effects,
perforation losses and restrictions due to completion hardware.
The total skin
can be considered as a summation of skins from various mechanisms, some of
which can be impacted by underbalanced operations. For example:
|

|
(9)
|
where:
|
s
|
=
|
total skin (all “skins” are dimensionless)
|
|
sM
|
=
|
mechanical skin (due to damage)
|
|
sPP
|
=
|
partial penetration skin (only part of a zone is
completed)
|
|
sQ
|
=
|
rate-dependent skin (due to turbulence)
|
|
sPERF
|
=
|
skin associated with perforating or completing
|
Mechanical Skin (Drilling/Completion Damage)
These skins develop during drilling, workover or
injection/production and are associated with the formation near the
wellbore. Undamaged, naturally
fractured reservoirs can have a slightly negative skin (anything beyond –3 is
probably induced). These reservoirs are extremely susceptible to drilling and
completion damage.
Consider the situation shown in Figure 4, where concentric
radial damage has been created by drilling and/or completing overbalanced. How do you characterize the skin?
Ø Let’s
suppose that we are dealing with permeable flow alone and that there is no
damage or improvement around the well.
Ø The
mechanical skin for such a case is 0.
Ø The
only pressure drop is due to flow through the porous medium. Denote this as 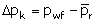 .
.
Ø If
there is skin present, the bottomhole injection pressure, for the same rate as
the undamaged case, will be lower or higher (stimulated or damaged,
respectively). Let’s denote this as pwfs.
Ø When
there is skin, the pressure drop from the undamaged part of the formation
(through the "damaged" zone) into the wellbore would be 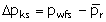 .
.
Ø You
can see that the difference between Dpk and
Dpks
indicates the pressure drop due to mechanical skin, giving Dps
= Dpks - Dpk
Ø If
you use Equation (6) you can estimate the skin as (laminar):
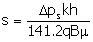
Ø If
you know, or can estimate, rs, you can estimate the permeability in
the damaged zone by using Dps in a steady-state version of
Darcy’s law:
|
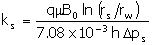
|
(10)
|
Ø If
you know, or can estimate, rs , Equation 7 can be used.
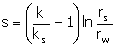
Ø
Finally, you can consider an equivalent wellbore
radius, using Equation 8, rwa = rw-s
Partial Penetration
Partial penetration or partial completion skin is associated
with drilling through only part, or completing only part, of a formation.
Though it may be most important during early time, it can be an issue through
the lifetime of a reservoir. This skin depends on the deviation of the well
through the target zone, the amount of formation penetrated during drilling
and/or the amount of formation open to the wellbore.
Rate-Dependent Skin
Rate-dependent skin is
associated with turbulent flow. Turbulent flow can be important in high-rate
wells – particularly for gas but also oil in some high rate situations. If this
is the case, the flow equation is modified to represent an additional pressure
drop. To account for turbulence in the previously developed relationships (see
Equation 1):
|
For single phase liquid
flow: 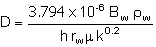
|
(11)
|
where:
|
ro
|
|
oil density at reservoir temperature and average pressure
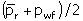 . .
|
For additional reading, refer to:
|
Jones, L.G.,
Blount, E.M., and Glaze, O. H.: “Use of Short Term Multiple Rate Tests to
Predict Performance of Wells Having Turbulence,” SPE 6133, SPE 51st
Annual Fall Meeting, New Orleans, LA (1976).
|

Figure 3. Schematic representation of mechanical skin
in a generic reservoir
Perforation/Completion Friction
Perforation friction can also impair injection. Perforation
friction - pressure drop due to flowing through the perforated, or other,
completion - can definitely be reduced by appropriate underbalanced completion,
in addition to an intelligent perforating program. According to Suman,
“Perforating is always a cause of additional damage in formation rocks.”4 Whether it is perforated overbalanced or
underbalanced, perforating compacts the formation around the perforations. This
compacted zone probably has an average thickness of 0.5 inches and the
permeability reduction averages 80%.
While compaction damage during perforating is anticipated
(regardless of the balance conditions), underbalanced perforating offers
significant advantages for removal of gun debris and damaged material and may
reduce the extent of the damaged zone. You can estimate pressure drop
associated with a perforated completion and infer the corresponding skin factor
using the methods described in Completion
Hydraulics.
Typically, pressure drop and skin estimates are based on the
premise that all guns fired properly and that all perforations are open. You
can infer the damage due to alone by measuring the total skin with some form of
well testing, isolating the skin due to turbulence and then subtracting the
skin due to perforating, partial penetration and wellbore geometry. Perforation
friction is often not adequately considered. Though it is often rather small,
there can be important exceptions, and you should include it in your
completions' design.
For now, consider the implications of the relationship shown
in Figure 4. This is the most basic perforation design plot, highlighting the
role of spacing. The trends are as you would expect – greater perforation
density generally leads to higher rates. Design methodologies are available for
spf, phasing, charge size, gun characteristics and balance. One of the more
difficult characteristics of a perforating program is to estimate how much the
near-perforation permeability is damaged and to what extent. In a well
consolidated formation, the damaged depth can be 0.5 inches and permeability
may be reduced to 10 to 25% of the virgin formation permeability (McLeod,
1983).
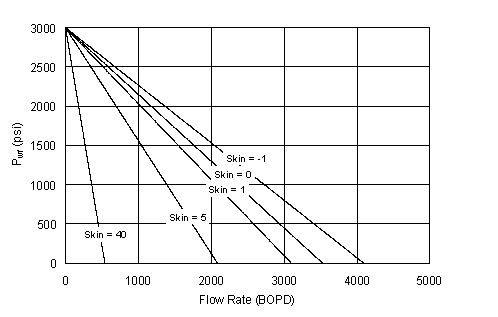
Performance relationships are impacted by skin. It is
important to minimize formation damage during all phases of drilling,
completion, and injection. For example,
Figure 1 is based on no skin, and Figure 5 shows the influence of skin on
performance.
Figure 4. Schematic
relationship showing the variation of total inflow with perforation density.
This curve is schematic. The particular
curve shape depends on the perforation and formation specifics and the degree
of underbalance during shooting.
Figure 5. Example
IPR curves for an oil well (ignoring dissolved gas for now) with different
values of total skin. Even modest skins can seriously impact productivity and
overall economics (i.e., the bottomhole flowing pressure must be lower to
achieve the same rate as the skin increases).
This example is for production.
Gas Flow and Turbulence
Flow mechanics in the reservoir, in the completions, and in
the production string are greatly complicated when turbulent flow occurs. For a dry gas or for a situation with a GOR >
30,000, recall that pseudo-steady-state gas flow can be expressed as:
|
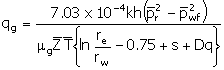
|
(12)
|
|
qg
|
=
|
gas flow rate (Mscf/D),
|
|
k
|
=
|
permeability (md),
|
|
h
|
=
|
thickness (feet),
|
|

|
=
|
average temperature (°R, °R = °F + 459.67), and,
|
|
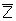
|
=
|
average compressibility factor (dimensionless) (Average
viscosity should also be considered.)
|
This equation can be written as:
|
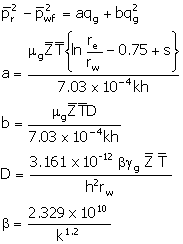
|
(13)
|
It is helpful to separate pressure drop due to turbulence
from skin arising from other sources so that you can assess the specifics of
the completion. The quadratic term on the right hand side of Equation 13
accounts for non-Darcy, turbulent effects. This relationship can be rearranged
by dividing both sides by the flow rate:
|
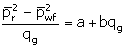
|
(14)
|
This equation is sometimes a more convenient form for
visualization because it can be expressed as a straight line (as shown in
Figure 8), and the term on the left-hand side of this equation can be
considered as a reciprocal injectivity or productivity index.
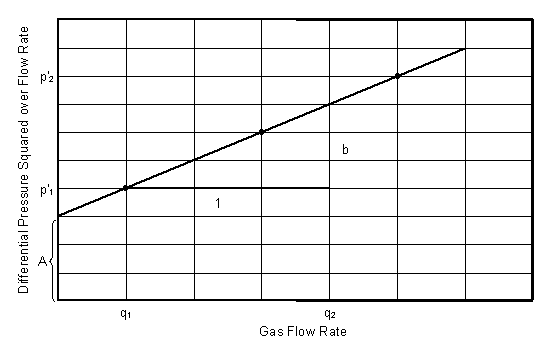
Figure 6. Variation
of injectivity/productivity index for gas as a function of the gas flow rate.
This type of plot is useful for identifying the presence of turbulence.
If this plot has a positive slope (as shown in Figure 6), turbulence is
indicated. Figure 7 shows how this type of plot can be useful for
discriminating between turbulence and other types of skin. In Figure 7, relationships are shown for
eight generic well situations in a hypothetical field – different wells are
indicated by the numbers on the plot. Wells 1 and 5 show no turbulent effects
because b = 0 (slope is zero). Wells
2 through 4 and 6 through 8 show increasing levels of turbulence. Why are the
two sets of curves different? There is greater skin (not associated with
turbulence) for Wells 5 through 8.
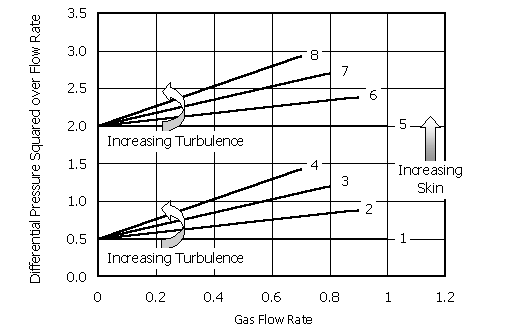
Figure 7. Variation
of injectivity/productivity index for gas as a function of the gas flow rate,
with varying degrees of turbulence and skin due to damage.
Evaluating the skin due to turbulence helps you to determine
whether the pressure drop is intrinsic to the formation and/or the completion
and cannot be overcome without stimulation. You can use simple diagnostic plots
to separate skin caused by turbulent flow from skin caused by damage and, to a
certain extent, skin caused by the completion itself. Similarly, you can use
simple methods to design the most effective completion (beforehand) and to
assess its effectiveness or the need for remedial measures (after the fact).
You can prepare the same types of plots for oil to separate
turbulence from other skins (turbulence is less common when oil is produced,
but it can occur). Recall that the slope b
in Figure 7 is indicative of the nature of the skin in the well. If b is high, it indicates high turbulence.
A large value of the intercept a
implies that the skin is high (not associated with turbulence) or that
permeability is low.
If the well has been fractured, you must consider other
factors.
Horizontal Wells
The relationships presented so far are for straight hole.
Various relationships have been extended to approximate flow in horizontal
wells. Be careful. Analytical relationships may be inadequate (A. Settari,
personal communication). Some of the
analysis techniques are summarized below.
·
Using numerical simulation, Bendakhlia and Aziz (1989)
suggested that:
|
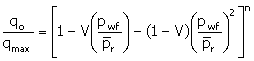
|
(15)
|
|
V
|
=
|
variable parameter in a modified Vogel’s equation
|
|
n
|
=
|
exponent in Fetkovich’s equation
|
To use this, recognize that there
are three unknowns (qmax, V, and n). At least three stabilized
flow measurements are required to build the IPR.
·
For pseudo-steady-state flow, Joshi (1991) presented an
approximate formulation:
|
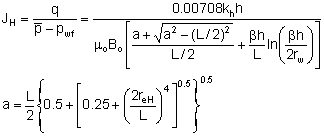
|
(16)
|
|
JH
|
=
|
Productivity/Injectivity Index (PI) for a horizontal well
section (BOPD/psi)
|
|
h
|
=
|
true vertical thickness of a zone (feet)
|
|
reH
|
=
|
drainage radius (feet)
|
|
kh
|
=
|
horizontal permeability (md)
|
|
kv
|
=
|
vertical permeability (md)
|
|
L
|
=
|
horizontal length (feet)
|
|
rw
|
=
|
wellbore radius (feet)
|
|
b
|
=
|
(kh/kv)0.5
|
Thomas et al. (1996) showed calculations of near-wellbore skin
and the non-Darcy flow coefficient (turbulence) for horizontal wells for
various drilling and completion scenarios. They provided analytical and
numerical solutions for near-wellbore skin and non-Darcy flow for horizontals
drilled underbalanced or overbalanced with various completion options. In particular, they explored the effects of
drilling overbalanced versus underbalanced and completing openhole with or
without a slotted liner or completing cased hole. This reference is
recommended.
According to Thomas et al., “Traditional formulations of
wellbore skin assume radial flow into a vertical wellbore, and must be
transformed to apply to horizontal wells.” In these formulations, adopt the
convention that the horizontal wellbore is oriented with the x-axis and its
length is L. k is the geometric mean of the two permeability components
perpendicular to the direction of the well. “Implementation of these terms
[skin terms] into different wellbore models results in different multiplying
factors on the skin and non-Darcy flow terms depending upon how a particular
well model was derived. This approach is different than the treatment for
vertical wells (Thomas et al., 1992) where the effect of partial penetration on
near-wellbore skin is included with the s and D terms.”
Available formulations, by various different authors, are
shown below. Thomas argued that there
were basically no significant predictive differences between any of the models.
Mutalik, et al., (1988) developed a relationship by using
the solution for a fully penetrating infinite conductivity fracture. For pseudo-steady state flow into a
horizontal well:
|
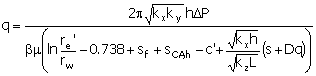
|
(17)
|
|
sf
|
=
|
skin for a fully penetrating vertical fracture
(dimensionless)
|
|
c’
|
=
|
horizontal shape factor in this model (dimensionless)
|
|
re’
|
=
|
effective drainage radius (feet)
|
|
b
|
=
|
a turbulence factor
|
|
s
|
=
|
mechanical skin (dimensionless)
|
|
kx
|
=
|
horizontal permeability in the direction of the well (md)
|
|
ky
|
=
|
horizontal permeability normal to the direction of the
well (md)
|
|
kz
|
=
|
is the vertical reservoir permeability (md)
|
|
L
|
=
|
is the length of the completed interval (feet)
|
|
sCa,h
|
=
|
is a skin associated with the drainage area’s shape (dimensionless)
|
Babu and Odeh (1989) developed an equation from the
classical vertical solution turned on its side, accounting for the resulting
geometry. Thomas et al. (1996) added mechanical skin to this relationship to
give the following equation:
|
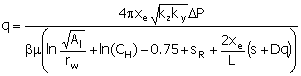
|
(18)
|
|
sR
|
=
|
partial penetration skin in the Babu and Odeh model
(dimensionless)
|
|
xe
|
=
|
half-length of the drainage area in the x-direction (feet)
|
|
Al
|
=
|
horizontal well drainage area (ft2)
|
|
CH
|
=
|
horizontal shape factor in the Babu and Odeh model
|
Economides et al. (1994) used a semi-analytical technique in
which an instantaneous point source analytical solution was integrated numerically
in time and space to give constant flux solutions for a horizontal well located
anywhere in the drainage volume of a uniformly heterogeneous reservoir with
three-dimensional permeability anisotropy. They used a horizontal shape factor
from Besson (1990). These solutions are
used to calculate constant pressure solutions for pseudo-steady-state:
|
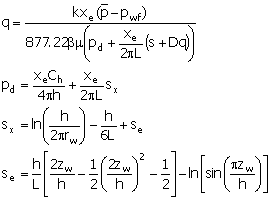
|
(19)
|
|
k
|
=
|
absolute permeability (md)
|
|
xe
|
=
|
drainage length in the x-direction (this is the well
direction)(feet)
|
|
sx
|
=
|
vertical skin effect (Kuchuk, 1995) (dimensionless)
|
|
se
|
=
|
term to account for vertical eccentricity (dimensionless)
|
|
sew
|
=
|
distance of the well from the center of the reservoir
(feet)
|
|
Ch
|
=
|
a horizontal shape factor in the Economides et al. model
(dimensionless)
|
There are certainly other analytical formulations. For
additional information, the reader can review Goode and Kuchuk, or Kuppe and
Settari, 1996.
Analytical and even numerical prediction of the behavior in
horizontal wells can be quite difficult. As Teichrob et al. (1998) state:
“Without some knowledge regarding inflow distribution and magnitude, accurately
predicting bottomhole pressure becomes problematic at best and impossible at
worst. At best, design considerations must focus on ‘dead’ or non-productive
holes, then attempt to bracket several flowing conditions recognizing differing
points of inflow and magnitude.” A
reasonable integrated approach can use information acquired during
underbalanced drilling. According to Butler et al. (1996). “For a number of years we have postulated
that sweet spots within a lateral section of a reservoir could be identified
(in real time while drilling) through superposition of elemental inflow
performance relationships. Using 50 meters as [an] elemental wellbore length,
the concept is as follows: element #1 is drilled and inflow is measured and
correlated to a given pressure drop. Injection ratios are changed, while still
honoring hole cleaning and bottomhole pressure constraints. New inflow rates
are measured and correlated to a different pressure drop. An inflow
relationship is therefore developed for element #1, which describes inflow over
a range of differing pressures. A new element is drilled. Because we have a
relationship that describes inflow over a range of pressure drawdown for
element #1, we are able to reconcile what the contribution of that previous
element should be based on the new pressure drops across the first element. Overall,
flow to surface can be measured and will be the sum of predicted inflow from
element #1 plus inflow from the newly drilled element.”
Multilaterals
Following horizontal wells, the next most recent trend in reservoir
exploitation has been to drill multilaterals. Some inflow performance
procedures have been formulated for multilaterals and branched wells (for
example, Larsen, 1996). These can be
useful in determining if underbalanced completion is merited.
Larsen used pseudo-radial skin factors for systems of
connected wells, intervals or fractures with a common bottomhole pressure or
potential. The approach assumes a certain distance between the midpoints of the
well elements (e.g. branches, drainholes, fractures, the well, or multiple
wells) and then assumes that the pressure development only depends on the
distance. Larsen stated, “Even relatively close to a horizontal well, it is,
for instance, possible to estimate the pressure development with negligible
error by using a fully penetrating vertical line well. Moreover, since the
line-source solution can be approximated with a simple logarithmic expression
at sufficiently later times, it is possible to combine the effect of, for
instance, several wells or branches by elementary methods.”
Larsen argued that you can apply the basic pseudo-steady
state equations (e.g. Equation 2 for a circular, bounded drainage area) to any
well configuration with some minimal distance between inner and outer
boundaries of the system. For cases with significant boundary effects occurring
before pseudo-steady-state flow (e.g., for a horizontal well approaching the
length of the reservoir in the direction of the well), you should use a direct
solution rather than analytical approximations. Regardless, for situations
where the equivalent wellbore radius remains within the drainage area, indirect
methods are acceptable.
By considering symmetrical characteristics in the well
system, Larsen implemented the basic analytical relationships for wells with
long horizontal branches in bounded reservoirs. For regular patterns of
branches or wells treated as a single drainage system, Larsen suggested
subdividing and adding the partial IIs. For nw wells:
|
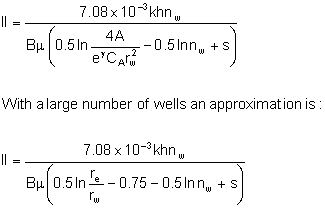
|
(20)
|
According to Larsen, “For wells with multiple branches, the
pressure transient behavior can be obtained by spatial superposition of
solutions for individual branches. The late time difference from the solution
of a fully penetrating vertical well can then be used to determine the
pseudo-radial system skin factor … of the given well configuration.” This
analysis is complicated for layered or heterogeneous reservoirs and at this
time it should consider only single layered systems with horizontal isotropy.
Other analytical formulations for evaluating transient
behavior in multiple laterals are available in the literature (for example,
Ozkan et al., 1997).
Obviously, these situations are so complex that simulation
is recommended. However, for back-of-the-envelope evaluations, methodologies
like this can be used for determining productivity, for building composite
performance curves, and for evaluating the contribution of mechanical skin
(which may be alleviated by underbalanced operations, if economically
appropriate).
Transient Performance Curves
Let’s take a step back. We have briefly summarized some of
the issues for relationships between pseudo-steady-state or steady-state flow.
The complexities for pseudo-steady-state flow in horizontal wells have been
indicated. You can see that developing performance curves for multilaterals
during pseudo-steady-state flow is even more complicated.
Most of the relationships shown to this point have been for
pseudo-steady-state or steady-state flow. When a reservoir is produced without
voidage replacement, the average reservoir pressure is reduced (i.e., transient
pressure behavior) and the inflows performance changes. The performance can
also change with time even if the average reservoir pressure does not change
significantly - the flow behavior is transient. During underbalanced drilling
and completion, flow usually is transient, but you can develop IPR curves for
any time in the productive life of a reservoir, as shown in Figure 8.
Wells initially start out under infinite acting radial flow
(unless the perforations or completed zone are very restrictive – spherical
flow). As the radius of influence approaches the boundaries, the flow regime
changes until pseudo-steady-state is reached. Further behavior depends on the
type of boundary (e.g., no flow, constant pressure, mixed, etc.). Regardless,
most drilling and completion scenarios can probably be reasonably represented
as infinite-acting radial flow. This flow condition in itself is transient.
Equation 3 showed relationships for how flow and/or pressure
change during this transient period. These are:
|
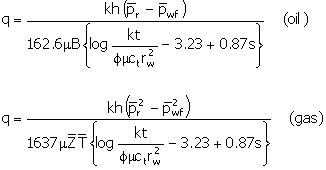
|
(21)
|
Figure 8. Typical
transient performance curves for a reduction in average reservoir pressure. You
can see that pressure-rate relationships change over the producing time. There are implications. For example,
behavior during a workover intervention may be different than during the
initial completion. This example is for
production.
Regardless of which technique you choose, you can develop
IPR curves for various values of drawdown, depletion, and time. Remember that m, B,
ct, and 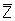 change with reservoir
pressure and drawdown.
change with reservoir
pressure and drawdown.
Summary
·
Most injection operations, but not all, will be in
pseudo-steady-state or steady-state regime. This is all premised on the
injection fluid properties being the same as the reservoir fluid properties.
·
If your reservoir is high permeability the period for
infinite acting radial flow (IAR) may be short.
·
As soon as the pressure disturbance caused by flow from
the well reaches the outer boundary, a transition period starts from infinite
acting radial flow, going to a pseudo-steady-state period, or to steady-state.
·
The pseudo-steady-state period occurs if a no-flow
boundary farthest from the well is reached by the pressure disturbance and the
entire area of influence is affected by injection. Rate and wellbore pressure
tend to stabilize.
·
When does pseudo-steady-state behavior start? As was
indicated in Equation 2:
|
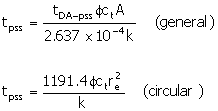
|
(22)
|
·
Can I develop performance curves for infinite-acting
conditions as a series of rate-pressure plots just using Equation 21 and
inputting different values of pwf? You can only do this to provide
rough indications of behavior because the transient effects are not properly
accounted for when the rate changes.
What Happens if the Reservoir is Layered?
In many cases, the reservoir encountered may not be
homogeneous. Consider the simple situation shown in Figure 9. The permeability
can be approximated as:
|
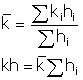
|
(23)
|
|
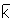
|
=
|
average permeability (md)
|
|
h
|
=
|
gross thickness (feet)
|
|
i
|
=
|
subscript denoting an individual layer
|
The situation is dramatically more complicated if there is
variable water or gas cut, different rates of depletion in different zones, and
crossflow. This is not to say that there are not some possible approximations.
Consider commingled injection (no vertical, in-reservoir crossflow) of two
zones. If the reservoir pressure in Zone 2 is less than that in Zone 1, net
production will not occur until the producing pressure, pwf is less than a critical value, p*wf. Above this pressure, fluid just goes from one
zone to the other. This “critical”
pressure is:
|

|
(24)
|
For this basic commingled case, you are able to construct
the performance curve for each zone and add the predicted rates at various
pressures less than p*wf. Somehow,
however, you have to know the properties of each zone (core analysis, logging,
production logging, PTA…) from this well or from offsets.
The previous sections provided a brief introduction to some of
the reservoir engineering considerations that are essential to effectively and
safely design any injection. Note that
this only covers matrix injection without a front. But the performance of the reservoir is only part of the whole
story. The other half of the story is that flow to the surface can be
restricted by the specific completion, the string in the hole, and the surface
facilities. This relates to the
hydraulic behavior of the completion itself and the tubing. Completion hydraulics are described first
and then tubing-related hydraulics are briefly covered.
Completion Hydraulics
After evaluating the pressure profile in the reservoir, the
next step in estimating potential well performance is to estimate the pressure
drop through the specific completion. The scenarios can range from barefoot to
gravel pack completions. You can assess barefoot completions using the methods
already described. This section covers both gravel pack and perforated
completions. Gravel pack completions are described for completeness and for the
possibility that they can be components in underbalanced interventions. You can
also use these examples to infer skins associated with slotted liners, screens,
etc.
Cased-Hole Gravel Pack Completion
For Oil or Water:
|

|
(25)
|
|
pwfs
|
=
|
sandface flowing pressure determined from the IPR (psia)
|
|
pwf
|
=
|
bottomhole flowing pressure (psia)
|
|
q
|
=
|
flowrate (BLPD)
|
|
m
|
=
|
viscosity (cP)
|
|
B
|
=
|
formation volume factor (RB/STB)
|
|
Lperf
|
=
|
distance from the outer screen diameter to the tip of the
perforation (feet)
|
|
kgravel
|
=
|
permeability of the gravel (md) (see Table 1)
|
|
Aperf
|
=
|
available area for access to the formation (total of the nominal
perforation cross-sectional areas through the perforated interval) (feet2)
|
|
bgravel
|
=
|
a turbulence term for the gravel
|
|
r
|
=
|
liquid density (lbm/ft3)
|
|
hperf
|
=
|
net perforated interval (feet)
|
|
nperf
|
=
|
shot density (spf)
|
|
dperf
|
=
|
perforation diameter (inches) (see Table 2)
|
|
dscreen
|
=
|
screen diameter (inches) (see Table 3)
|
Table 1. Typical Gravel
Permeability
|
Gravel Size
(U.S. Mesh)
|
Average Porosity
(%)
|
Average Permeability
(darcies)
|
|
40-60
|
39.8
|
69
|
|
20-40
|
40.9
|
171
|
|
10-20
|
40.5
|
652
|
|
8-12
|
41.5
|
1969
|
|
6-10
|
42.0
|
2703
|
|
|
Table 2. Typical Perforation
Information
|
Gun Size
(inches)
|
Casing Size
(inches)
|
Average Perforation Diameter
(inches)
|
Penetration
(inches)
|
|
|
Average
|
Longest
|
|
Through Tubing Retrievable
|
|
1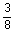
|
4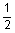 casing casing
|
0.21
|
3.0
|
3.3
|
|
1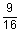
|
5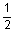 casing casing
|
0.24
|
4.7
|
5.4
|
|
1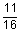
|
4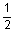 to 5 to 5 casing casing
|
0.24
|
4.8
|
5.5
|
|
2
|
4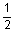 to 5 to 5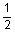 casing casing
|
0.32
|
6.5
|
8.1
|
|
2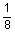
|
2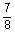 tubing to 4 tubing to 4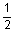 casing casing
|
0.33
|
7.2
|
8.1
|
|
2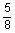
|
4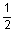 casing casing
|
0.36
|
10.3
|
10.3
|
|
Through Tubing Expendable
|
|
1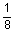
|
4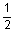 casing casing
|
0.19
|
3.1
|
3.1
|
|
1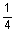
|
2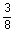 tubing?? tubing??
|
0.30
|
3.9
|
3.9
|
|
1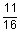
|
2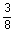 tubing to 5 tubing to 5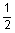 casing casing
|
0.34
|
6.0
|
8.1
|
|
2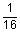
|
5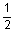 to 7 casing to 7 casing
|
0.42
|
8.2
|
8.6
|
|
2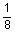
|
2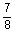 tubing tubing
|
0.39
|
7.7
|
8..6
|
|
Retrievable Casing Guns
|
|
2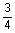
|
4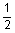 casing casing
|
0.38
|
10.5
|
10.5
|
|
2
|
4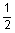 casing casing
|
0.37
|
10.6
|
10.6
|
|
3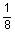
|
4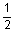 casing casing
|
0.42
|
8.6
|
11.1
|
|
3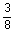
|
4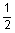 casing casing
|
0.36
|
9.1
|
10.8
|
|
3
|
4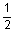 and 5 and 5 casing casing
|
0.39
|
8.9
|
12.8
|
|
4
|
5 to 9 to 9 casing casing
|
0.51
|
10.6
|
13.5
|
|
5
|
6 to 9 to 9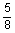 casing casing
|
0.73
|
12.3
|
13.6
|
|
|
Table 3. Common Screen
Diameters for Inside Casing Gravel Packs
|
Casing
|
Maximum Screen Diameter
|
Commonly Used Screen Diameter*
|
|
OD
(inches)
|
Weight
(lbf/ft)
|
ID
(inches)
|
Pipe OD
(inches)
|
Wire OD
(inches)
|
Pipe OD
(inches)
|
Wire OD
(inches)
|
|
4
|
9.5
|
3.548
|
1
|
1.815
|
1
|
1.815
|
|
4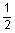
|
11.6
|
4.000
|
1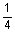
|
2.160
|
1
|
2.160
|
|
5
|
18.0
|
4.276
|
1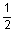
|
2.400
|
1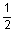
|
2.400
|
|
5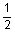
|
17.0
|
4.892
|
2
|
2.875
|
2
|
2.875
|
|
6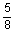
|
24.0
|
5.921
|
3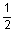
|
4.000
|
2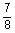
|
3.375
|
|
7
|
29.0
|
6.184
|
3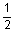
|
4.000
|
2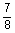
|
3.375
|
|
7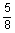
|
33.7
|
6.765
|
4
|
4.500
|
2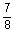
|
3.375
|
|
8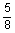
|
36.0
|
7.825
|
5
|
5.500
|
2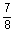
|
3.375
|
|
9
|
47.0
|
8.681
|
5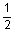
|
6.000
|
2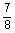
|
3.375
|
|
*Different screen diameters may be
required for specific circumstances such as larger diameter production
tubing, multiple gravel packs, etc.
|
For Gas
|
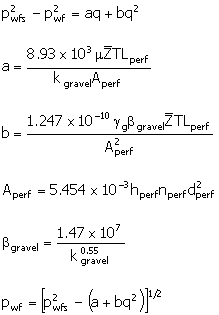
|
(26)
|
|
pwfs
|
=
|
sandface flowing pressure determined from the IPR or
deliverability equations (psia)
|
|
pwf
|
=
|
bottomhole flowing pressure (psia)
|
|
q
|
=
|
volumetric flowrate (MscfD)
|
|
m
|
=
|
gas viscosity at the mean pressure (cP)
|
|
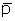
|
=
|
mean pressure, 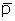 = =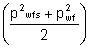 (psia) (psia)
|
|
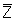
|
=
|
real gas deviation factor (dimensionless) at T, 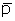
|
|
T
|
=
|
temperature (°R
= °F +
460)
|
|
Lperf
|
=
|
distance from the outer screen diameter (feet) to the tip
of the perforation (feet)
|
|
dscreen
|
=
|
screen diameter (inches) (see Table 3)
|
|
kgravel
|
=
|
permeability of the gravel (md) (see Table 1)
|
|
Aperf
|
=
|
available area for access to the formation (the total of
the nominal perforation cross-sectional areas through the perforated interval)
(feet2)
|
|
bgravel
|
=
|
a turbulence term for the gravel
|
|
hperf
|
=
|
net perforated interval (feet)
|
|
nperf
|
=
|
shot density (spf)
|
|
dperf
|
=
|
perforation diameter (inches) (see Table 2)
|
|
gg
|
=
|
gas gravity (dimensionless, air = 1.0)
|
Example: Calculating IPR for a Cased-Hole Gravel Pack
Completion
Calculate Performance Relationship for this Example as
Follows:
kgravel = 652 darcies, 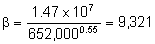 .
.
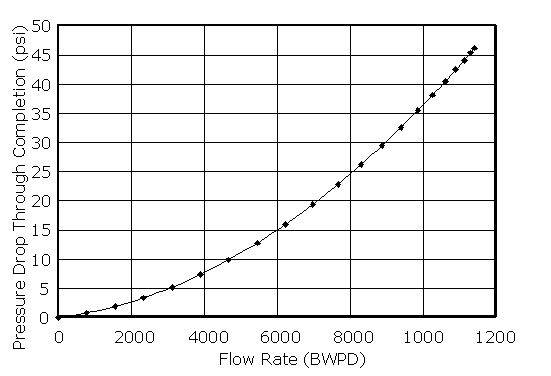
The pressure drops due to the completion itself can be
plotted to indicate the contribution from the completion more specifically, as
shown in Figure 10.
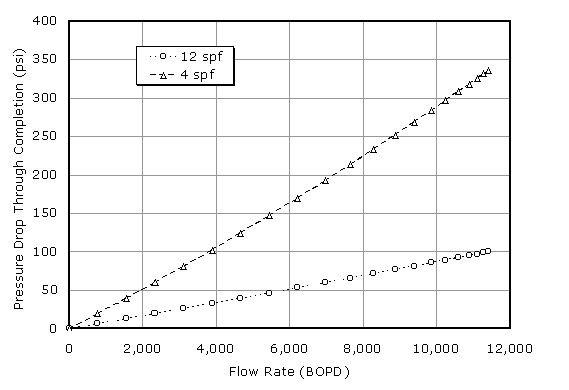
Figure 10. Pressure drop due to the cased-hole,
gravel pack completion in the example case. The baseline reservoir performance
assumed no mechanical skin (no plugging), but formation damage skin can be
considered. Just use a skin term when the formation performance is calculated.
Cased, Cemented and Perforated Completion
The previous gravel pack completion example included some
obvious simplifications about the effectiveness of the perforations. It assumed
that the perforations themselves did not damage the formation in any way. In
reality, the skin associated with perforating can be surprisingly important.
Perforation pressure drop (from which skin can be calculated) can be inferred.
Some approximations for a cased-cemented-perforated completion are shown below.
For Oil or Water
The procedure is not unlike that taken for the cased hole
gravel pack, with the exception of the presumed flow regime around the
perforation tunnel. Assuming that there is no interaction between perforations,
a first-order assumption is that there is radial flow from each perforation.
Assuming this:
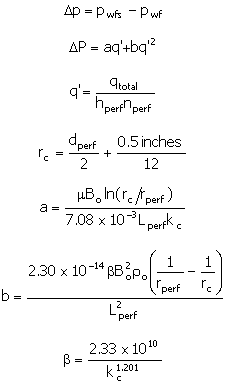
|
(27)
|
|
Dp
|
=
|
pressure differential across the completion (through the perforation
and the surrounding crushed/damaged zone)
(psi)
|
|
q’
|
=
|
flow rate per perforation (BOPD/perforation)
|
|
qtotal
|
=
|
total flow rate (BOPD)
|
|
b
|
=
|
turbulence factor
|
|
rperf
|
=
|
perforation radius (feet)
|
|
dperf
|
=
|
perforation diameter (feet)
|
|
nperf
|
=
|
perforation density (spf)
|
|
hperf
|
=
|
net perforated length (feet). Partial penetration of a deviated well will create additional
skin
|
|
m
|
=
|
viscosity (cP)
|
|
Bo
|
=
|
Formation Volume Factor (RB/STB)
|
|
rc
|
=
|
radial extent of the crushed zone from the centerline of
the perforation tunnel (feet). The example shown is for a situation where it
is assumed that the crushed zone around the tunnel is 0.5 inches thick. You can
use other values, if available. This is a common default assumption. As can
be seen in the equation, the crushed zone thickness is converted to feet by
dividing by 12.
|
|
kcf
|
=
|
permeability of the perforation damaged zone (md). This is
determined by multiplying the native reservoir permeability (k) by a damage
factor.
|
|
ro
|
=
|
oil density (lbm/ft3)
|
The permeability of the compacted zone is commonly assumed
to be a fraction of the nominal reservoir permeability. A rule-of-thumb is:
|
kc = 0.1k Overbalanced
kc = 0.4k Underbalanced
|
(28)
|
This in itself shows a key reason for perforating
underbalanced – the degree of damage in the compacted zone can be significantly
less than when perforating is done balanced or overbalanced.
For Gas
The approximations shown above are a generic and ideal
approximation for liquid flow through perforations. Similar concepts can be
applied for gas. If the perforations are considered to not interfere with each
other, a first-order assumption is that there is radial flow from each
perforation. Based on this assumption:
|
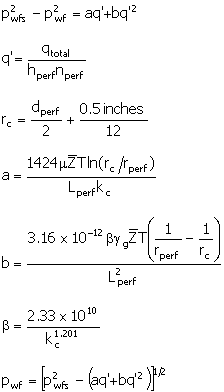
|
(29)
|
|
q’
|
=
|
flow rate per perforation (MscfD/perforation)
|
|
qtotal
|
=
|
total flow rate (MscfD)
|
|
nperf
|
=
|
perforation density (spf)
|
|
hperf
|
=
|
net perforated length (feet)
|
|
m
|
=
|
viscosity (cP)
|
|
b
|
=
|
turbulence factor
|
|
rperf
|
=
|
perforation radius (feet)
|
|
dperf
|
=
|
perforation diameter (feet)
|
|
rc
|
=
|
radial extent of the crushed zone from the centerline of the
perforation tunnel (feet). The example shown is for a situation where it is
assumed that the crushed zone around the tunnel is 0.5 inches thick. You can
use other values, if available. This is a common default assumption. As can
be seen in the equation, the crushed zone thickness is converted to feet by
dividing by 12.
|
|
Lperf
|
=
|
perforation length (feet)
|
|
kc
|
=
|
permeability of the perforation damaged zone (md). This is
determined by multiplying the native reservoir permeability (k) by a damage
factor. The same default assumptions for the damage factor are made as for
oil.
|
|
gg
|
=
|
gas gravity (dimensionless, air = 1)
|
|
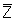
|
=
|
mean real gas deviation factor (dimensionless)
|
|
T
|
=
|
Temperature (°R
= °F +
460)
|
Calculating Performance for a Cased and Perforated Oil Well
Table 4. Basic Reservoir and
Completions Data
|
Parameter
|
Value
|
Calculations
|
|
Average reservoir
pressure
|
2000 psi
|
|
|
Water viscosity
|
1 cP
|
|
|
Water formation volume
factor
|
1 RB/STB
|
|
|
Water Density
|
54.67lbm/ft3
|
|
|
Well Orientation
|
vertical
|
|
|
Perforation Density
|
12 spf or 4 spf
|
|
|
Perforated Interval
|
30 feet
|
|
|
Casing
|
6.625"
|
|
|
Gun
|
5"
casing gun
(underbalanced)
|
|
|
Permeability
|
100 md
|
|
|
Drainage Radius
|
1140 feet
|
|
|
Bubble Point Pressure
|
1200 psi
|
|
|
Drilled Diameter
|
9 inches
|
|
The pressure drops due to the completion itself can be
plotted to indicate the contribution from the completion more specifically, as
shown in Figure 11.
Figure 11. The pressure drops due to the completion
in the example case. The baseline
reservoir performance assumed no skin, but formation damage skin can be
considered.
Other Completions
Methods were shown for estimating the pressure drop for
two generic completion types - a cased and perforated completion and a gravel
pack completion. The gravel pack
calculations shown were for an ideal pack without any associated damage to the
perforations. For the gravel pack, the
basis for the calculation was to assume that there was linear flow along the
perforation tunnel and through the gravel.
This analysis did not incorporate any damage to the pack or to the
perforations. To accommodate damage to
the gravel pack itself (either due to placement or fines, etc.) the gravel pack
permeability can be reduced. To account
for perforation damage, split the problem into two parts – first, calculate the
pressure drop for linear flow through the gravel in the pack and in the
perforation tunnel. Then, calculate the
pressure drop through a compacted zone around a perforation as shown in the
second example. Then combine the
pressure drops or skins.
These conceptual methods can provide guidelines for
determining pressure drops through other types of completions. Consider an openhole gravel pack. This situation could be considered as a
two-part reservoir with radial flow (one permeability zone is the gravel and
the second is the formation itself).
This problem can be solved by using some of the formulas presented
earlier. One approximation is to use:

For example, let k be the formation permeability with a
value of 1000 md. Let ks be
the gravel pack permeability – assume that the pack has been placed perfectly
and the gravel has a permeability of 650 darcies. At this point, be a little careful - use rw as the
outer diameter of the screens. Use rs
as the drilled diameter of the wellbore.
Let’s assume a 9-inch hole, giving rs = 9/(2 x 12) = 0.375
feet. If a 3 3/8-inch diameter screen wire
wrapped screen is used (and pressure drop is ignored through the screen – for
demonstration purposes at least), the artificial wellbore radius can be taken
as 3.375/(2 x 12) = 0.141 feet. The
skin would be:
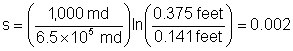
Granted, this demonstration shows negligible skin. It becomes more significant if the formation
permeability is higher, if the gravel is damaged with placement or injection
fluids, if the formation has been damaged by fluids, solids and inadequately
cleaned up, if plugging or other mechanisms are impairing the screens
themselves – and so on.
Other types of completions provide specific pressure
drops. Kaiser et al., 2000, provide an
excellent presentation of the methodologies that can be used for optimizing
slotted liner selection.
“The primary factors considered in [slotted liner] design
are sand control, inflow resistance and cost.
Inflow performance is usually considered to be controlled by the open
area exposed to the reservoir, and sand control governed by slot opening
size. These become competing
considerations in reservoirs with fine sands because slot density must be
increased to maintain open area if slot size is reduced to control sand.”
The pressure drop through this type of completion is not
only a function of the slot, but also the flow convergence in the sand that
packs around the slots. “In fact, the
flow loss through an open slot is negligible compared with that induced by the
flow disturbance associated with the slot.”
You can visualize the difference between uniform flow into a barefoot
completion, with a slight convergence into the hole, with the much more extreme
convergence that concentrates flow into a slot at similar rates. These convergence effects can lead to
pressure drops that bear consideration during planning stages. You might think that fewer larger slots
would have less flow resistance than more smaller slots for the same open
area. This presumption ignores what
Kaiser et al. indicate as the most important component of slot-induced loss –
this being the convergence of flow in the sand that is packed around the
slots. In fact, they indicate that this
is why wire wrapped screen are so effective; because the “slots” are very close
together and this minimizes the extent of flow convergence and its associated
pressure loss. [Note that Kaiser was
commenting on production.]
Kaiser and his colleagues outlined a combined empirical,
analytical and numerical program where they optimized liner characteristics for
Marathon’s South Bolney field. Their
analysis model combined the radial Darcy flow relationships, a mechanical skin
factor that is associated with flow convergence and flow along the completion
itself (see the section on Wellbore Hydraulics). They called the slot component of the skin factor the slot factor
and provided some illustrations of its relative contribution. “The slot factors calculated from the flow
convergence analysis are dimensionless numbers that are used with the near-wellbore
permeability to calculate the pressure loss induced by the slots.”
This paper is recommended reading. These authors also discussed the standard engineering
considerations of optimizing the completion to avoid slot plugging and the
considerations that may be taken for evenly distributing flow along a long
slotted liner section in a horizontal or extended reach well.
Convergence through limited access in the completion
hardware is the essential issue. In
effect, this is analogous to partial penetration. These effects can be compounded if blank sections are run within
the liner section. Blanks can be used
for load control devices. The inflow
performance is impacted by the reduction in the net production interval. There is local flow convergence at the slots
themselves and larger scale convergence to the slotted intervals. Rough approximations of the “partial
coverage” skin from this effect (for example, ignoring axial flow) were
provided as:
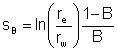
where:
B = the coverage ratio is B.
Manufacturers should be able to provide you with the skin
that is associated with a specific completion.
Of course, plugging of the screens themselves compounds these
skins. We all know that this is not a
trivial issue. A recent paper by Asadi
and Penny, 2000 demonstrates some of these issues. One of the most important aspects of this paper related to the
methodologies and effectiveness of cleanup techniques on screens that were
damaged while being run – this brings us back to some of the advantages of
underbalanced operations where it may be possible to mitigate the damage by
running in certain less damaging fluids.
Standard sand control considerations are published elsewhere
(for example, Penberthy and Shaughnessy, 1992.) The work of Asadi and Penny is valuable because large-scale
empirical measurements were made on commercial products (20/40 PMF – porous
fiber material – equivalent to a 20/40 sand, 20/40 Stratapack, and 0.008-in
gauge wire wrap Prepacked with 40/60 mesh resin coated sand). These components were exposed to a formulated
drill-in fluid containing drill solids.
Various cleanup techniques were then attempted (10% HCl; enzyme breaker
followed by 10% HCl; acid activated breaker, followed by 10% HCl, with and
without water backflow. The efficiency
of some of the evaluated hardware was low and cleaning was never 100% effective
– sometimes much less. The products
were vulnerable to plugging and cleanup under ideal laboratory conditions was
never ideal. Consider all methodologies
for reducing the degree of plugging in the first place. Also remember that the pressure drop even in
clean screens will be elevated when turbulent flow exists. Asadi and Penny, 2000, indicated pressure
drops of between 0.05 and 0.1 psi at an injection rate of between 9 and 18
BLPD/ft of length. Turbulent flow will
elevate these values even for clean screens.
The issue of turbulent pressure losses applies to all types
of completions, including, as we have seen cased and perforated
situations. The reader may wish to
review numerical work by Behie and Settari, 1993. Numerical models such as these can also be used to evaluate the
influence of collapsed and filled perforations – another potentially
significant skin component – even if shot underbalanced or maybe because they
were, collapsed and infilled perforations can add significantly to pressure
drops that are experienced.
It all boils down to calculating skin. This section was intended to illustrate
concepts. These days in most cases, you
would have software available. However,
without understanding underlying concepts, using commercial or internal
software is inefficient at best, and possibly dangerous.
Using the concepts shown, you can estimate the degree of
damage due to the completion and the skin due to the completion itself. For an excellent summary of skin associated
with perforating, refer to Chapter 6.5.3 in Bell et al., 1995. For a complete discussion of sand control
issues, refer to Penberthy and Shaughnessy, 1992. For cogent discussions of the reservoir engineering aspects of
various completions, refer to Beggs, 1991, and/or Golan and Whitson, 1991).
There are methods for estimation of the pressure drop
through the reservoir and the completion.
To complete the analysis of well performance you must next consider the
effects of wellbore hydraulics.
Wellbore Hydraulics
There are methods for estimating pressure changes in the
reservoir and across the completion. You will need to complete the final
component of the well performance analysis – estimating the pressure drop in
the wellbore and at the surface. The pressure regime in the tubing or annulus
is governed by hydrostatic, frictional, and acceleration forces. This section
shows you how to approximate these effects for single phase and multiphase flow
in the wellbore.
The key to estimating pressure drop is determining an
accurate bottomhole pressure. Consider the simplest situation – single phase
flow. You can estimate bottomhole pressure, (pBH or pwf)
from surface pressure psurface using the following equation:
|
pBH
= psurface + pHydrostatic – pFriction
|
(30)
|
pHydrostatic is the hydrostatic head of the fluid
in the tubing and/or annulus and pFriction is the loss in pressure
due to friction loss during flow.
Hydrostatic Pressure
The hydrostatic component is the pressure exerted by the
column of liquid/gas in the wellbore. This pressure is a function of the fluids
present and consequently can vary, from a static bottomhole value if the well
is shut-in (or not flowing), to a hydrostatic pressure reflecting changing
fluid ratios during flow. Under static conditions, without flow, there are no
frictional contributions and a static bottomhole pressure is calculated from a
summation of surface pressure and the hydrostatic head.
Calculating the static bottomhole pressure for a
liquid-filled wellbore involves simply multiplying the fluid gradient (density)
times the true vertical depth.
For a vertical well filled with gas, the static condition is
given by integrating the density over the depth interval. The form of the
integration is given by:
|
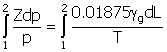
|
(31)
|
where:
|
Z
|
=
|
gas deviation factor
(dimensionless). Z can be regarded as
a term by which pressure must be corrected to account for departure from the
ideal gas equation pV = ZnRT
|
|
p
|
=
|
absolute pressure (psia)
|
|
¡g
|
=
|
specific gravity of the gas (dimensionless, air = 1.0)
|
|
T
|
=
|
absolute temperature (°R)
|
|
L
|
=
|
length (feet)
|
If the temperature and pressure are taken at an average value
(indicated by the bar in the following equation), the following equation
accounts for gas compressibility:
|
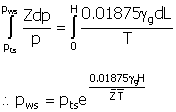
|
(32)
|
where:
|
pws
|
=
|
static bottomhole pressure (psia)
|
|
pts
|
=
|
static wellhead pressure (psia)
|
|
H
|
=
|
true vertical depth (feet)
|
The temperature is commonly taken as the arithmetic mean of
the bottomhole and wellhead temperatures, assuming a linear variation with
depth. 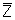 is taken as the value at the arithmetic mean temperature and
the arithmetic mean pressure. Because of the interrelationships between
parameters, this bottomhole pressure equation is generally solved by
trial-and-error. While you likely have a numerical model or spreadsheet to do
these calculations, it is instructive to understand some of the background. The
iterative steps are:
is taken as the value at the arithmetic mean temperature and
the arithmetic mean pressure. Because of the interrelationships between
parameters, this bottomhole pressure equation is generally solved by
trial-and-error. While you likely have a numerical model or spreadsheet to do
these calculations, it is instructive to understand some of the background. The
iterative steps are:
If you use the method of Sukkar and Cornell, 1955, trial and
error procedures are not required. For even more precise calculations, you can
use the method proposed by Cullender and Smith (1956). Good references on this
topic are Bradley, 1991 and Ikoku, 1980.
Friction
Using the methods in the previous section, you can estimate
the hydrostatic head for a well containing liquid, gas, or multiphase fluids
during a completion operation. The next component to consider in calculating
the bottomhole pressure is the friction that exists when fluids are moving. The
complex frictional forces of fluids flowing in a wellbore depend on the type of
fluid flow regime. This section considers frictional effects for:
Single Phase Liquid Flow
For liquid flow in the wellbore, the pressure drop per unit
length (for friction effects only) is given by the following equation:
|
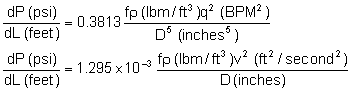
|
(33)
|
|
dP
|
=
|
pressure change (psi)
|
|
dL
|
=
|
length of the segment over which the pressure drop is
calculated (feet)
|
|
p
|
=
|
density (specific gravity x 62.4) (lbm/ft3)
|
|
f
|
=
|
Moody friction factor (dimensionless)
|
|
v
|
=
|
velocity (ft/second)
|
|
D
|
=
|
equivalent diameter (inches)
|
The term “equivalent diameter” is used to discriminate
between pipe flow and annular flow. For conventional pipe flow, Equation 33 is used
and D is the internal diameter of the pipe over the length being evaluated. For
annular flow, the effective diameter is:
|

|
(34)
|
For annular flow, use D = Douter – Dinner in
the second form of Equation 33. In the first form of Equation 33, replace D5
with (Douter – Dinner)3 x (Douter +
Dinner)2.
The length term in Equation 33 is based on measured depth
because friction acts over the full length of the string (unlike hydrostatic head,
which is based on true vertical depth). If there are changes in string
dimensions and/or inclination, it is common practice to divide the well up into
individual increments and sum the friction over the individual discrete
lengths. If the wellbore contains compressible fluids and you use fundamental
friction equations, you must discretize the wellbore (divide it into discrete
lengths).
As reflected in Equation 33, during flow, irreversible energy
losses occur. With the exception of completely laminar flow, these energy
losses cannot be predicted theoretically and are usually accounted for by using
the friction factor (as shown in Equation 33). For consistency, only the Moody
friction factor will be used (the Moody friction factor is four times the
Fanning friction factor (fF)). The friction factor (f) and the
relative roughness (e/D)
are related to the Reynolds’ Number. The Reynolds’ Number is calculated by:
|
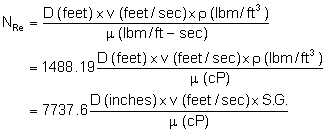
|
(35)
|
|
e
|
=
|
absolute roughness (feet)
|
|
D
|
=
|
diameter (feet)
|
|
S.G.
|
=
|
specific gravity (dimensionless)
|
|
v
|
=
|
velocity (feet/second)
|
|
NRe
|
=
|
Reynolds Number (dimensionless)
|
|
m
|
=
|
viscosity (1bm/ft-sec or cP)
|
|
Flow
Regime
|
Reynolds
Number
|
Moody
Friction Factor
|
Comments
|
|
Laminar
|
<
2000
|
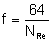
|
Independent
of roughness
|
|
Critical
26
|
2000
< NRe < 4000
|

|
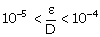
|
|
Transition26
|
4000
< NRe < (200D/e)1.16
|
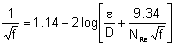
|
Colebrook (1939)
|
|
Turbulent26,28
|
NRe
> 4000
|
 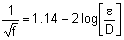
|
Nikuradse
|
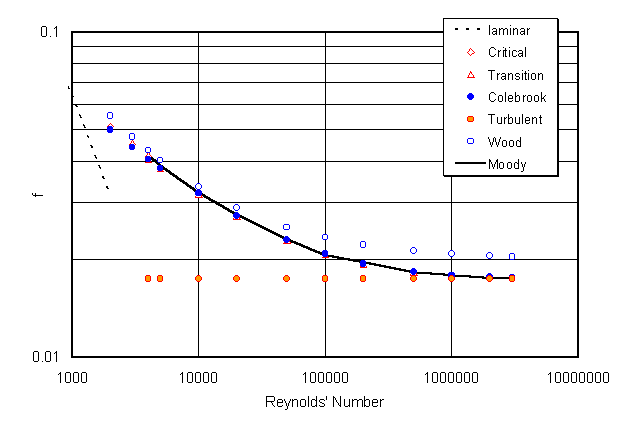
Figure 12. Comparison of Moody friction factors for
various calculation methods for a relative roughness of 0.0006. Woods’ curve is
an explicit approximation of Colebrook’s relationship.
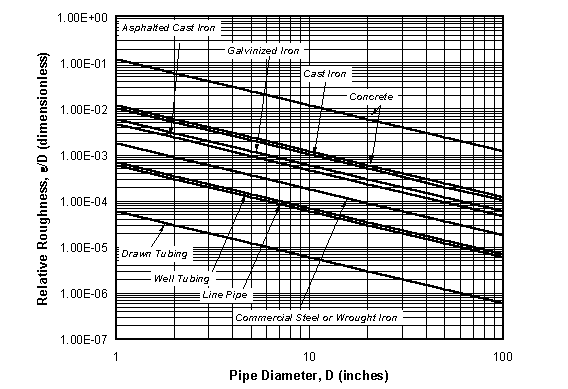
Though roughness is quite difficult to determine,
particularly for tubulars that have been in service for some time, some
guidelines are available. Figure 13 shows an example. Using these guidelines,
you can estimate frictional pressure loss using Equation 33 and Table 5. It is
usually appropriate to discretize the flow path and solve over various
increments, using the previous increment to provide an upstream boundary
condition. Commercial codes are available for these calculations.
Single Phase Gas Flow
For steady-state flow, the energy balance is given by
(notice that this contains the hydrostatic head component).
|

|
(36)
|
|
r
|
=
|
fluid density (lbm/ft3)
|
|
p
|
=
|
pressure (psia)
|
|
v
|
=
|
average fluid velocity (ft/sec)
|
|
a
|
=
|
correction factor to compensate for variation of velocity
over the tubing cross-section, varying from 0.5 for laminar flow to 1.0 for fully
developed turbulent flow. A value of 0.90 is commonly used for practical gas
flow problems.
|
|
H
|
=
|
distance in the vertical direction (feet)
|
|
f
|
=
|
Moody friction factor (dimensionless)
|
|
D
|
=
|
inside pipe diameter (feet)
|
|
L
|
=
|
length of the flow string (feet), L = H for a vertical
section
|
|
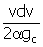
|
=
|
pressure drop due to kinetic effects,
|
|
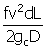
|
=
|
pressure drop due to friction,
|
|
ws
|
=
|
mechanical work done on or by the gas (ws = 0)
|
|
g
|
=
|
acceleration due to gravity (ft/s2)
|
|
gc
|
=
|
conversion factor (32.17 lbm - ft/1bf s2)
|
Ignoring the kinetic energy term and integrating over an
interval from point “1” to point “2” gives:
|
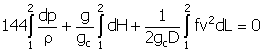
|
(37)
|
Combining using oilfield units and assuming constant
temperature over an interval of interest:
|
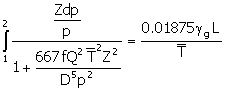
|
(38)
|
where:
|
p
|
=
|
pressure (psia)
|
|
Q
|
=
|
gas flow rate (MMscfD)
|
|
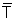
|
=
|
average temperature over the distance L, (°R)
|
|
L = H
|
=
|
vertical distance (feet)
|
|
D
|
=
|
inside diameter of the pipe (inches)
|
Unfortunately, without assumptions or numerical solution,
this equation cannot readily be integrated.
Smith (1950) proposed an approximate solution (based on the Weymouth
equation):
|
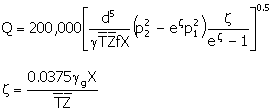
|
(39)
|
|
Q
|
=
|
volumetric flow rate measured at 14.656 psia and 60°F
(scfD)
|
|
T
|
=
|
effective average temperature (°R)
|
|
Z
|
=
|
effective compressibility factor for the gas
|
|
d
|
=
|
pipe ID (inches)
|
|
p2
|
=
|
sandface pressure at depth X (psia)
|
|
p1
|
=
|
wellhead pressure (psia)
|
|
gg
|
=
|
gas gravity (dimensionless, air = 1.0)
|
|
X
|
=
|
difference in elevation between points 1 and 2 (feet)
|
|
f
|
=
|
Moody friction factor (dimensionless)
|
There are numerous other approximate or numerical
formulations. Most of these are available in or superceded by commercial software
packages. For example:
·
Poettmann (1951) derived an expression accounting for
the variation of the compressibility factor. It can be applied to deviated
wells.
·
You can use a modified version of the Sukkar and
Cornell Method (see Katz et al., 1959) for straight or inclined holes. Their
relationship assumes steady-state, single phase flow, negligible kinetic
energy, constant temperature at some average value, and a constant friction
factor over the length of the conduit.
·
Two-step approximations can be done using the Cullender
and Smith method.
·
There are other relationships: the Panhandle formula;
the Ford, Bacon and Davis formula; and the Clinedinst flow equation.
Multiphase Flow
The procedures for evaluating multiphase flow are
substantially more complicated than those for single-phase flow. The level of complexity for multiphase flow
is so high that numerical analysis and/or correlations are commonly used for
frictional evaluations. Some of the
possible correlations that you can use for forecasting pressure drop are:
·
Duns and Ros (1963) can be used for certain vertical
flow situations.
·
Orkiszewski (1967) can be used for certain vertical
flow situations. Orkiszewski outlined
methods for addressing flow of discrete bubbles, slug flow where the gas phase
is more pronounced, a transition flow (transitional from continuous liquid to
continuous gas) and mist flow where the gas phase is continuous and most of the
liquid is present as entrained droplets.
Computational versions of this method are widely used, with some
specific limitations.
·
Hagedorn and Brown, 1965, is probably recommended for
most vertical flow situations. It was
developed from experimental measurements in an instrumented 1500-ft deep
well. Neither liquid holdup or flow
pattern was measured but correlations were developed by assuming that the
two-phase friction factor could be obtained from the Moody diagram based on a
two-phase Reynolds Number. Refer to
Appendix A in Beggs 1991. This is
recommended reading on this topic.
·
Beggs and Brill, 1973, deals with any inclination,
two-phase flow. Liquid holdup and
pressure gradients were measured for flow of air and water in a laboratory
environment, for inclinations between horizontal and vertical. Liquid holdup is the fraction of an element
of pipe that is occupied by liquid at some instant.
·
Mukherjee and Brill, 1983, developed a procedure for
wells of any inclination with two-phase flow, and,
·
Dukler, 1959, provided correlations for horizontal
flow.
The Hagedorn and Brown correlation
commonly
gives good results for most situations.
There are some simpler methods as well. You can use the Poettmann-Carpenter method
for vertical multi-phase flow.
Recognize that other methods, such as Hagedorn and Brown, are more (and
sometimes much more) accurate. Poettmann-Carpenter determined an f’
factor empirically and correlation charts were prepared for various tubing
sizes on which were plotted the total mass-producing rate QM versus
the pressure gradient dP/dh.
Computational routines are commercially available (and
should be used) for multiphase flow for high profile situations. For rapid calculations, in addition to the
Poettmann and Carpenter procedures, an extensive set of gradient curves has
been generated and published by Brown (1984).
Gradient curves have been generated for various tubing/annulus
dimensions, rates and the specific fluid properties.
Restrictions
Inevitably, there will be pressure losses in in-line
restrictions, including subsurface safety valves, surface or bottomhole chokes,
valves and fittings, etc., Beggs provides a clear discussion. Some of the key
points are summarized below.
Single Phase Gas Flow through
Surface Chokes
Flow through a restriction can be critical or subcritical
(sonic or subsonic). When the flow is
critical, any downstream disturbance will not affect the upstream pressure or
the rate. Since chokes are intended to
control rate, they usually are designed for critical flow. “A rule-of-thumb for distinguishing between
critical and subcritical flow states that if the ratio of downstream pressure
to upstream pressure is less than or equal to 0.5, then the flow will be
critical. This is a closer approximation for single-phase gas than for
two-phase flow.”
|
|
(40)
|
where:
|
qsc
|
=
|
volumetric gas flow rate (Mscf/D)
|
|
d
|
=
|
I.D. of bore open to gas flow (inches)
|
|
gg
|
=
|
gas specific gravity (dimensionless, air = 1.0)
|
|
k
|
=
|
ratio of specific heats = Cp/Cv
(dimensionless)
|
|
p1
|
=
|
upstream pressure (psia)
|
|
p2
|
=
|
downstream
pressure (psia)
|
|
T1
|
=
|
upstream temperature (°R)
|
|
Z1
|
=
|
compressibility factor at p1 and T1
(dimensionless)
|
|
CD
|
=
|
discharge coefficient (empirical, dimensionless)
|
|
Tsc
|
=
|
standard absolute temperature base (°R)
|
|
psc
|
=
|
standard absolute pressure base (psia)
|
|
y
|
=
|
p2/p1
|
|
yc
|
=
|
critical pressure ratio (dimensionless)
|
When no information is available, the restriction is short
with slightly rounded openings and critical flow conditions exist, an
approximation is (using a generic default value of CD = 0.82):
|
|
(41)
|
Single-Phase Liquid Flow through Surface Chokes
The following equation may be used (assuming subcritical
flow, if necessary, a default value for the discharge coefficient can be used,
CD = 0.85):
|
|
(42)
|
where:
|
qL
|
=
|
liquid flow rate (STB/day)
|
|
d
|
=
|
choke diameter (inches)
|
|
p
|
=
|
psi
|
|
S.G.
|
=
|
liquid specific gravity
|
Two-Phase Flow through Surface Chokes
An empirical relationship in the critical regime is:
|

|
(43)
|
where:
|
pi
|
=
|
upstream pressure (psia)
|
|
qL
|
=
|
liquid flow rate (STB/day)
|
|
R
|
=
|
gas/liquid ratio (scf/STB)
|
|
d
|
=
|
choke diameter (inches)
|
Values of a, b and c have been proposed by different
investigators. For very rough
approximations, try using a = 1.89, b = .00386 and c = 0.546. Sachdeva (1986) presented a more rigorous
model.
Gas Flow Through a Subsurface Safety Valve
Flow will generally be subcritical - minimal downhole
restriction is desirable. You can
iterate and solve using the API relationship:
|
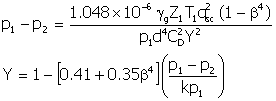
|
(44)
|
where:
|
p1
|
=
|
upstream pressure (psia)
|
|
p2
|
=
|
downstream
pressure (psia)
|
|
g
|
=
|
gas gravity (dimensionless, air = 1.0)
|
|
Z1
|
=
|
gas compressibility at p1 and T1
|
|
T1
|
=
|
upstream temperature (°R)
|
|
qsc
|
=
|
gas flow rate (Mscf/D)
|
|
b
|
=
|
d/D
|
|
d
|
=
|
bean diameter (inches)
|
|
D
|
=
|
pipe inside diameter (inches)
|
|
CD
|
=
|
discharge coefficient (API suggests 0.9)
|
|
Y
|
=
|
expansion factor (dimensionless). The expansion factor determination is
iterative and may be calculated from Equation 44. Its value ranges between 0.67 and 1.0. For quick estimates, a
default value of 0.85 is often used.
|
|
K
|
=
|
the ratio of specific heats of the gas.
|
Two-Phase Flow Through a Subsurface Safety Valve
For two-phase flow through a subsurface safety valve, you
can use:
|
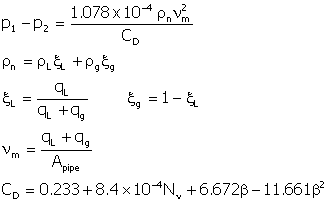
|
(45)
|
where:
|
rn
|
=
|
no-slip density
(lbm/ft3)
|
|
qL
|
=
|
"in-situ" total liquid rate
|
|
qg
|
=
|
"in-situ" gas rate
|
|
nm
|
=
|
mixture velocity through the choke (ft/sec)
|
|
p1
|
=
|
upstream pressure (psi)
|
|
p2
|
=
|
downstream pressure (psi)
|
|
CD
|
=
|
discharge coefficient
|
|
Nn
|
=
|
qg/qL = (1-lL)/lL
|
|
lL
|
=
|
qL/(qL+qg)
|
|
b
|
=
|
d/D
|
|
d
|
=
|
choke diameter
|
|
D
|
=
|
tubing inside diameter
|
All the fluid properties necessary for calculating the
density and velocities are evaluated at upstream conditions of pressure and
temperature. p1 is iteratively determined from a known p2.
Pressure Losses Through Valves and Fittings
The energy losses associated with bends and other
restrictions are considered to be supplemental to those predicted by
Bernoulli's basic equation and its standard representation using Moody's
friction factor. To account for these
additional pressure losses, the concept of a loss coefficient is used. Typically, the loss coefficient is indicated
as K. In simplified terms the pressure
loss for flow with bends and with other in-line obstructions can be expressed as:
|
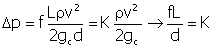
|
(46)
|
|
d
|
=
|
diameter of pipe
|
|
f
|
=
|
friction factor for pipe flow
|
|
L
|
=
|
length of pipe
|
|
K
|
=
|
resistance coefficient depending on the type or size of
fitting
|
An equivalent length, Le, can be calculated for
each fitting by using the friction factor calculated for flow in the pipe. All
the Le values can then be added to the actual pipe length for the
pressure drop calculation. K values
have been determined for single-phase flow and they are similar to values for
two phase flow (for example, 0.15 for a gate valve, 0.2 -0.3 for elbows, 3.0 -
5.0 for globe valves, 6.0 - 8.0 for check valves). The pressure drops will commonly be small enough to be ignored. A
more basic fluid mechanics approach is provided by Granger, 1985. Granger indicated the loss coefficient for a
rounded elbow could be determined from empirical relationships.
|
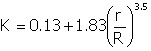
|
(47)
|
The degree of pressure loss due to bending is generally
taken to be a function of R (the radius of curvature and r the inner radial
dimension of the pipe. The term R/r is
known as the relative radius. For large
values of R/r, such as those which would be associated with the transitional
segment of a horizontal well, Rankin et al., 1989, proposed a loss coefficient
which is empirically correlated to the relative radius, a friction factor (f), bend angle in degrees and a
correction coefficient which depends on both the bend angle and R/r. These relationships were empirically
developed using data for water in fully developed turbulent flow and are
therefore relevant to conventional fluids (as opposed to lightened
fluids). The transition from horizontal
to vertical flow in the annulus is particularly sensitive to momentum flux –
“the tendency of the fluid to surge as head is overcome.” This is atttributable to the transition from
a somewhat static pressure regime in the horizontal segment to a sudden
reduction in momentum as the fluid is forced to travel upward.
Additional pressure drops that can be considered are
associated with tapered strings, tubing restrictions, the wellhead and any
horizontal lines or obstructions at the surface. Tapered strings can be evaluated numerically or published
gradient curves can be used. The
gradient curves for the specific tubular or casing dimensions are used in
combination by manipulating the effective depth (using the bottom run depth of
an upper tubing as the top of the section below).
Various restrictions to flow can be present - e.g., safety
valves, tubing nipples, downhole chokes.
Some manufacturer information is available. Similar information can be acquired for wellhead/BOPRBOP etc.
restrictions. Horizontal surface lines
can be represented using one of the methods that have been described above.
Using Tubing Intake Curves (Injection or Production)
Regardless of which method you use to estimate pressure
drops, you will need to determine hydrostatic pressure and friction at various
flow rates. Using your selected method,
you must generate tubing intake curves
to represent the flowing bottomhole pressure versus rate for the particular
tubing/annulus situation. Your tubing
intake curves will be based on the specific set of parameters that you define
(e.g., wellhead pressure, diameters, lengths, fluid type, etc.). Once you have defined these parameters, you
will construct a table of bottomhole pressure versus rate. Finally, you will plot the tubing intake
curves. An example is shown in Figure
14.
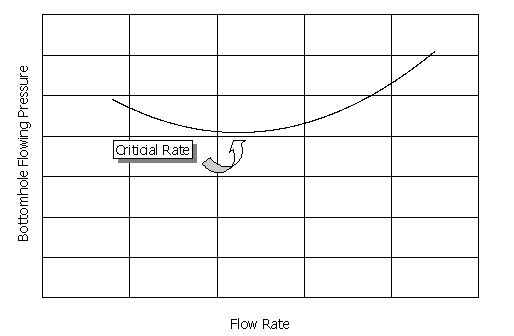
Figure 14. An
example tubing intake curve.
Tubing intake curves depend on a number of environmental
parameters. For example, different
tubing intake curves will exist for different wellhead pressures (refer to Figure 15).

Figure 15. Various tubing intake curves for different
flowing wellhead pressures. As pwf
decreases, the wellhead pressure also decreases.
The tubing intake curve (flow rate that the tubing can
accommodate) is also influenced by the size of the tubulars (refer to Figure
16).
Figure 16. Schematic change in tubing intake curves
for different size tubing.
You will recall that there are methods for inferring the
drop in pressure for flow through the formation, and through the
completion. You can also see from the
example tubing intake curves that there can be further restrictions associated
with flow in the wellbore. Because the
formation, completion, and wellbore pressure drops are not independent, you
must consider them using a systems approach.
You can use Nodal AnalysisTM principles and techniques to
evaluate the individual and combined effects of these parameters on well
performance.
Nodal Analysis
Nodal AnalysisTM was originally developed by
Flopetrol Johnston. Nevertheless, the concepts are universally applicable and
used by all service and operating companies.
In this method, you represent the reservoir-completion-string-surface
components by nodes that can be found in different parts of the well. A node is any point at which a pressure drop
is evidenced. Next, you evaluate the
pressure drops at all points and determine an equilibrium situation. Finally, you can determine the maximum
potential injection.
The performance relationships indicate the flow rates that a
formation can deliver and they can account for the effect of a particular
completion. The tubing intake curve
accounts for the flow rate the string/annulus can accommodate. You must superimpose the performance relationship
and tubing relationships to determine rate and pressure.
A simple example of using Nodal AnalysisTM or
related concepts is shown in Figure 17.
This schematic example is for a hypothetical injector. The effect of the perforation density has
been exaggerated for illustrative purposes.
A tubing intake curve developed for a particular combination of fluids
is superimposed on the IPR curves.
Using these data and the bottomhole pressure range, injection rate is
predicted. Expected wellhead pressures
can be determined by varying input into the calculation of the tubing intake
curve.
Figure 17. Hypothetical injection well. Several performance curves are shown for
various perforating programs. Several
tubing intake curves are superimposed for varying wellhead pressures. Intersections indicate anticipated pressures
and flow rates.
You can use Nodal AnalysisTM or equivalent
methods to evaluate potential well performance. If these programs are not available, do the appropriate
calculations in a spreadsheet.
References
1.
Good, P.A. and Kuchuk, F.J.:
“Inflow Performance of Horizontal Wells,” paper SPE 21460 (1991).
2.
Kuppe, F. and Settari, A.:
“A Practical Method for Determining the Productivity of Multi-Fractured Horizontal
Wells,” CIM Edmonton 96, Edmonton, Canada (April28-May 2, 1996) and JCPT
1998.
3.
Kaiser, T.M.V., Willson, S., and Venning, L.A.: “Inflow
Analysis and Optimization of Slotted Liners,” paper SPE 65517, 2000 SPE/PS-CIM
Int’l Conf on Horizontal Well Technology, Calgary, Canada, November 6-8.
4.
Asadi, M. and Penny, G.S.: “Large-scale Comparative Study of
Pre-Packed Screen Cleanup Using Acid and Enzyme Breaker,” 2000 IADC/SPE Asia
Pacific Oil and Gas Conf. Exhib, Brisbane, Australia, October 16-18.
5.
Penberthy, Jr., W.L. and Shaughnessy, C.M.: Sand Control, SPE
Monograph Series, Richardson, TX (1992).
6.
Behie, G.A. and Settari, A.: “Perforation Design Models for
Heterogeneous Multiphase Flow,” paper SPE 25901 presented at the 1983 SPE Joint
Rocky Mountain Regional/Low Permeability Reservoir Symposium, Denver, CO, April
26-28.
7.
Duns, H., Jr. and Ros, N.C.J.: Sixth World Petroleum Congress,
Section 2, Paper No. 22, Frankfurt, Germany (1963).
8.
Orkiszewski, J.: JPT., 19, 829 (1967).
9.
Hagedorn, A.R., and Brown, K.E.: JPT, 16, 203 (1964);
17, 475 (1965).
10.
Beggs, D.H. and Bril, J.P.: “A Study of Two-Phase Flow in
Inclined Pipes,” SPE 4007, JPT (1973).
11.
Mukherjee, H. and Brill, J.P.: “Liquid Holdup Correlations for
Inclined Two-Phase Flow,” SPE 10923, JPT (1983).
12.
Dukler, A.E.: Chem. Eng. Progress, 55(10), 62 (1959).
13.
McLennan, J.D., Carden, R.S., Curry, D., Stone, C.R. and
Wyman, R.E.: Underbalanced Drilling Manual, Gas Research Institute,
Chicago, IL (1997).
14.
Brown, K.E.: “The Technology of Artificial Lift,” Volume 4,
Pennwell, Tulsa, OK (1984).
15.
Sachdeva, R., Schmidt, Z., Brill, J.P. and Blais, R.M.:
“Two-Phase Flow Through Chokes,” SPE 15657, paper presented at the 1986 (61st)
Annual Tech. Conf. Exhib., New Orleans, LA.
16.
Granger, R.A.: Fluid Mechanics, Dover Publications, New York,
NY (1995).
17.
Rankin, M.D., Friessenhahn, T.J. and Price W.R.: “Lightened Fluid Hydraulics and Inclined
Boreholes,” SPE 18670, paper presented at 1989 SPE/IADC Drilling Conf., New
Orleans, LA, February 28 – March 3.
18.
Supon, S.B. and Adewumi, M.A.: “An Experimental Study of the
Annulus Pressure Drop in a Simulated Air-Drilling Operation,” SPE Drill. Eng.
(March 1991) 74-80.
19.
Wang, Z., Rommetveit, R., Bijleveld, A., Maglione, R. and
Gazaniol, D.: “Underbalanced Drilling Requires Downhole Pressure Management,” Oil
& Gas J. (June 16, 1997) 54-60.
![]() . Assume that there
is no skin (damage) or turbulence and that the well is drilled to 6 inches in
diameter. What sort of flow rates should you anticipate?
. Assume that there
is no skin (damage) or turbulence and that the well is drilled to 6 inches in
diameter. What sort of flow rates should you anticipate?