Basic Description of the Model
PWFRAC was developed for the PEA-23 project and is not in the open literature. All of the information presented here is from the feature article in the October 1999 PWRI Newsletter (Volume 1, No. 3).
Coupling of the pore fluid movement, pore pressure change, and stress changes associated with injection operations are incorporated in the model. Both internal formation damage and external cake are considered. When the open gap (the part of the fracture that is open between the filter cake on the fracture walls) does not extend to the tip of the fracture, the pressure-flow relationships along the open fracture gap satisfy the usual equations for viscous hydraulic flow between two surfaces. The pressure within the closed gap (designated as a tip plug) may have different pressure profiles, depending on the filter cake permeability. Opening of the fracture is computed from pressure along the fracture, based on poroelastic theory, resulting from Darcy flow in the formation. The fracture propagation criterion is based on a stress intensity factor. The filter cake buildup is linked to the amount of solid particles that are deposited by PW entering the formation at the fracture face. Erosion of particles, caused by shear stresses on the filter cake surface, and the pressure drop across the filter cake are also considered. The model also provides a detailed description of the near-tip region. The simulator provides the following predictions, as a function of time during the injection period:
Ø The injection pressure that is required to maintain a given injection rate,
Ø The length and width of the created fracture,
Ø The filter cake thickness and the open gap along the length of the fracture,
Ø The impaired permeability of the formation and the extent of this formation damage.
Fracture Propagation, Filter Cake Build-up and Formation Plugging During PWRI
Produced water (PW) injection offers an acceptable means of disposing of the produced water and may provide an opportunity for a water drive when applied in waterflooding. The required rate of produced water injection can be anticipated using the expected pore volume replacement ratio and water cut estimated from the production forecast. Fracturing is likely to occur during PW injection at voidage replacement rates.
The extent (size) of the induced fracturing will significantly impact this process. Therefore, it is necessary for well injectivity planning and fracture sizing to have an accurate estimate of the pore pressure, the rock's mechanical properties, and the minimum in-situ stress in the injection horizon. This collective information can be used to estimate the required injection pressure and the number of injectors throughout the production period. . Well planning and design can also benefit from predictions concerning the histories of the injector performance and the length of the created fracture. As a result, the waterflood planning cycle efficiency would be increased.
It is generally accepted that PW injection will lead to plugging of fractures and damage of injection zone permeability. The engineering problem faced by the operator is reduced to establishing the balance between two competing mechanisms. The first mechanism is related to the well injectivity improvement that may result from any fracturing associated with produced water injection. The competing mechanism results from plugging of the near crack tip region and the impairment of reservoir performance (permeability) around the fracture caused by water contaminant invasion of the injection horizon.
In the present article, we will confine the discussion to fracture propagation and its impact on well injectivity, under conditions of produced water injection in permeable reservoirs. Results of such analyses, in conjunction with experimental determinations, can provide estimates of filter cake permeability [if history matching is done, indications can be provided by the model alone, but, uniqueness is not guaranteed] and thickness, as well as the magnitude of permeability impairment around the fracture and the extent of the impairment zone.
Injector Fracturing Concepts
The objective of this article is to illustrate how fractures propagate during produced water injection. The role of porous formation mechanics on the interaction between a permeability-damaged zone around the fracture and a plug at the fracture tip is investigated. The article discusses the four concepts listed below:
Concept 1 The application of fracture mechanics techniques to hydraulic fracturing during the initiation of clean water injection and continuing through the life of the reservoir. Fracture mechanics can be used to predict the relationships between the injection rate, the size of the hydraulic fracture and the required injection pressure for clean water.
Concept 2 As injection proceeds, particles in the produced water are deposited in the injection formation horizon and a "damaged" zone forms around the hydraulic fracture surface. These deposits decrease the permeability of the zone and tend to increase the required injection pressure (for a fixed injection rate). Considerations must be given to the water quality (concentrations and characteristics of the damage-causing contaminants) and its relationship to formation damage.
Concept 3 A second characteristic of the continuing injection process is that a plug of produced water particles can collect at the tip of the hydraulic fracture. This plug restricts flow at the crack tip and also tends to increase the injection pressure that is required to dispose water at a given rate and also cause the fracture to propagate.
Concept 4 The two combined phenomena (indicated in 2 and 3 above) affect fracture propagation. Although both phenomena tend to increase the required injection pressure for a given injection rate, their influences on the local stress state (and their impact on the criteria for crack propagation) are quite different.
Fracturing Propagation Models for PW Injection
Fracture propagation during produced water injection in a permeable reservoir presents an added dimension to the problems encountered in applying fracture mechanics concepts to rocks. Coupling of the pore fluid movement, pore pressure change, and the stress changes associated with an injection operation must be incorporated in any analysis. The impact of water contaminants on plugging of the fracture and/or the formation depends on the injected water quality. General understanding gained from past experience and published data, as well as from earlier JIP work, provides the following insights into well fracturing during constant rate injection of produced water:
1. Fracture propagation during waterflooding using clean water requires injection pressures that are far in excess of those required during hydraulic fracturing conditions at a constant specified injection rate. A decrease in formation permeability or an increase in the injection rate will reduce the required pressure for fracture propagation at the same injection rate. If there is less fluid lost to the formation, pressure will develop in the fracture to facilitate propagation – this can occur if the rate is higher (poroelastic considerations, if the formation is less permeable and/or if cake develops along the fracture surface.
2. The presence of contaminants in the injected water will have two competing effects (tip plugging versus fracture face impairment) depending on where these particles are deposited.
3. Fracture extension during produced water injection operations may be significant without apparent changes in well injectivity, injection rate or pressure.
4. Fracture tip plugging by solids will lead to a higher required propagation pressure during waterflooding in comparison to the clean fracture tip case.
5. Formation permeability damage around the fracture will tend to facilitate fracture propagation during constant rate injection operations. The extent of the permeability reduction and the magnitude of the damage in the permeability impairment zone will both significantly impact the injection operations and will, in general, lead to a decrease in the required fracture propagation pressure.
6. Under constant injection rate, injector performance (for example, the injectivity index) can be maintained fairly constant, while both tip plugging and permeability damage occur. This can occur by fracture propagation without significant change in injection pressure. The two phenomena may actually be in balance.
7. Fracture growth might allow the operator to inject lower quality produced water for a longer period of time without adversely impacting injector performance (different water qualities significantly affect injectivity).
8. Conclusion #7, above, is not true if vertical conformance or aerial sweep become negatively impacted by the extent of fracturing in the injector. Care should be taken when interpreting PW injector data to allow for estimation of the fracture size.
9. Fracture propagation criteria for produced water injection can be best verified by comparison with available well performance records.
For predicting the behavior of a vertical fracture, propagating in a horizontal reservoir layer as a result of PW injection, a simulator must take into account the following phenomena:
1. Loading of the formation caused by the water flow during leakoff,
2. Permeability damage from produced water particles deposited in the formation during injection,
3. Filter cake build up on the fracture surface and plugging at the fracture tip.
These features are required for the simulator to reliably compute a fracture's dimensions and a well's response during injection. The simulator predictions need to be consistent with a set of field observations. This is demonstrated in the current article by several illustrative examples. The simulator must provide the following predictions - as a function of time during the injection period:
1. The injection pressure that is required to maintain a given injection rate,
2. The length and width of the created fracture,
3. The filter cake thickness and the open "gap" along the length of the fracture,
4. The impaired permeability of the formation and the extent of this formation damage.
To achieve the above, the simulator must represent the following six physical requirements and these must be satisfied simultaneously:
1. The poroelastic solution for the opening of a fracture subjected to arbitrary stresses/body forces, resulting from Darcy flow in the formation.
2. The fracture propagation criteria. These may be related to the stress intensity factor, KI, or other equivalent conditions.
3. The flow of fluid leaking off inside the injection zone. This flow most likely satisfies Darcy's law. The gradient of the pore pressure at the fracture face (within the damaged zone) is proportional to the rate of migration of the fluid that has leaked off (away from the fracture) and the impaired permeability.
4. The pressure-flow relationships along the open fracture gap (the open fracture width) must satisfy the usual equations for viscous hydraulic flow. Both laminar and turbulent flow regimes must be considered.
5. The filter cake buildup should be linked to the amount of solid particles that is deposited by water entering the formation at the fracture face. Erosion of particles, caused by the shear stress on the filter cake surface, and the pressure drop across the filter cake must also be accounted for.
6. Alteration of the formation permeability, by the produced water particles that are deposited in the formation, must be taken into account.
General Observations
As the fluid flows in the pores, the pore pressure is increased and the effective compressive stress in the matrix is reduced. Note, however, that depending on the diffusivity and poroelastic characteristics of the formation, the total stress can increase due to poroelastic effects. The stress distribution in the matrix is altered, and there are associated displacements that tend to close the fracture. The fracture itself is responding to the local total stress field. The situation is more complicated when a filter cake and altered formation permeability are present.
When the open gap (the part of the fracture that is open between filter cake on the fracture walls) does not extend to the end of the fracture, the pressure within the closed gap (designated as a tip plug) could be constant and equal to the pressure at the tip of the open gap. The tip plug region may have other pressure profiles depending on the filter cake permeability. If the formation layers bounding the fractured horizontal layer are sufficiently "strong" (or the stresses in these bounding layers are large enough), the fracture can be contained within the injection horizon. In a containment situation, the bounding zones cause a stiffening influence to the fracture propagation within the injection layer - with a consequent increase in injection pressure (all other factors being equal).
Filter Cake Behavior
A filter cake model for produced water injection depends on the particular volumetric fraction of the solids in the water entering a particular section of the fracture surface that is assumed to remain on the surface of the fracture (external cake). The remaining solids must pass along the fracture and may cause tip plugging, or, especially at early exposure times, form an internal cake. The solid material that collects on the fracture surface forms an external filter cake. The filter cake thickness should be determined in the simulator and with experiments and back-analysis, along with the permeability for the filter cake. Both of these quantities are needed for determining the pressure gradient in the filter cake as a result of fluid leakoff into the formation.
The solid material that is deposited on the fracture surface causes the effective fracture width to be reduced, leaving an open gap for flow along the fracture. When the volume rate of flow into the fracture is specified, reduction in the width of this gap can lead to increased fluid velocity along certain regions of the fracture. When the velocity in this effective fracture width is sufficiently high, material on the surface of the filter cake can be dislodged and swept into the flow along the gap. A criterion for "sweeping" material off the filter cake is required.
Formation Permeability Damage
When solids-laden produced water flows through a porous formation, some of the solids are deposited in the porous material. Some of the produced water particles become lodged in pores and do not move with the fluid. As flow continues, an equilibrium is reached between the concentration of particles trapped in the formation and those flowing with the fluid.
Consider the case where produced water, with a constant solids concentration, is entering a formation with no "fixed" (lodged, trapped…) particle concentration. After some time, solids concentrations in the formation can be expected decrease away from the fracture face. With time, solids concentrations in the formation, at a fixed position, will approach equilibrium values.
Parameter Interrelationships During Fracture Propagation Scenarios
In order to gain some physical insight into the more general case of a porous material where there is a damaged zone, a rough approximation is considered here. The results give a feeling for the influence of the actual damaged zone.
Consider that there is
a porous skin (internal and external filter cakes) at the surface of the
crack. Fluid pressure drops across
this skin as the fluid flows from within the crack into the porous material
(Figure 1). This skin represents
the collection of particles from the produced water that has accumulated at and
near the crack surface. Although
the mechanism for the pressure drop across this skin depends on many factors,
the pressure drop is taken here as a fraction, b, 
, of the internal crack pressure, pi,
or the injection pressure.
Additionally, the volume rate of flow, Q, into the formation is reduced
by the factor 
, compared to the case with no porous skin.
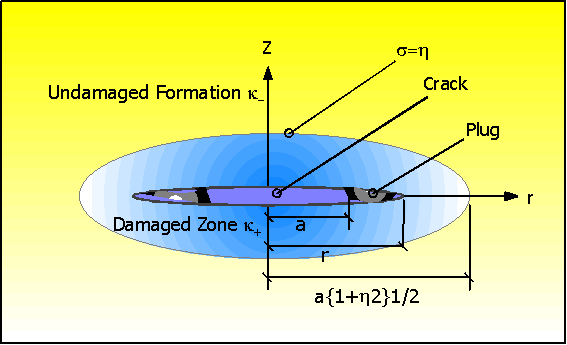
Figure 1. Schematic representation of a PWRI fracture.
(Use the symbol R on the figure like in the text instead of symbol r )
For a constant injection rate, there is a considerable increase in the stress intensity factor, KI as the skin factor increases (b).
For fixed values of n, k, KIc and Q, the dependence of the crack radius, a, and the crack pressure, pi, can be determined at incipient crack propagation. For example, consider the case of constant values for the injection rate (Q), the critical stress intensity factor (KIc) and the permeability to viscosity ratio (k). As b increases, the crack length (aA) grows while the crack pressure (aB) decreases. As b changes from 0 to 0.3 the crack length increases by about a factor of 3 while the crack pressure drops by about a factor of 2 (refer, for example, to Figures 2 and 3). “These results are related to a penny-shaped crack model and I feel that the pressure decrease has more to do with this frac geometry than with plugging effects.”[1]
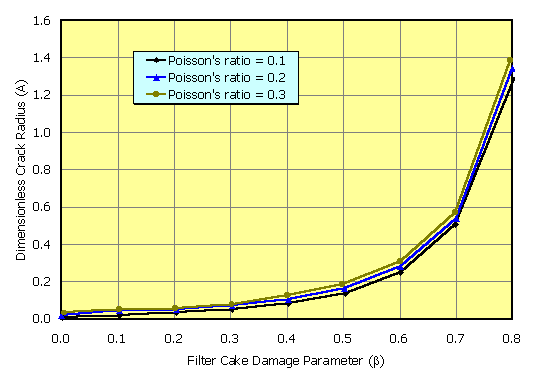
Figure 2. This figure shows a plot of A (dimensionless crack radius) versus b for three values of Poisson's ratio. The plot illustrates the interplay between poroelastic and filter cake effects. The crack radius increases with increasing damage.
Figure 3. This is an example plot of B versus b for the indicated values of Poisson's ratios. For the case of constant injection rate, Q, the curves show the relationship between the injection pressures and the amount of damage. According to this model the injection pressure, pi, will decrease as the damage increases (due to damage and the geometry of the fracture). The pressure decrease may have more to do with the volume of the fluid lost than the extent of the damage. The argument for this is that in conventional hydraulic fracturing simulations, excess pressure (for a contained two-dimensional fracture) decreases with increasing fluid loss. However, the increase in length shown in Figure 2 can be directly correlated with the plugging effects of the solids.
Porous Material Solution with Damaged Zone and Crack Tip Plug
The schematic in Figure 1 considers the following scenarios:
1. A plug of length R - a occupies the crack tip(s). In this representation, the crack radius is R while the radius that is open for "fluid occupancy in the crack" is a. There is no fluid flow into the injection zone from the crack surface between the radii a and R.
2. A damaged zone of finite extent is introduced around the crack. The damaged zone is an ellipsoid occupying the region around the fracture. All quantities in the damaged zone are designated with subscripted plus signs. For example, P+ is the pore pressure in the damaged zone and k+ is the permeability to viscosity ratio in the damaged zone. The corresponding quantities outside of the damaged zone are designated with subscripted minus signs. The elastic properties, l, m and n (Lamé’s constants and Poisson’s ratio) of the poroelastic material are the same in the damaged and undamaged zones.
From Figure 1, the relations between a, R, and h may be written as
are factors for the sizes of the tip
plug and damage zones.
is
the elliptical coordinate of the damage zone.
is
the permeability damage factor
This configuration can be used to predict fracture propagation parameters at a fixed injection rate, Q, and a fixed crack radius, R, (tip plugging and efficiency could be restricting growth) while h is increased (a greater extent of the damage zone) and g is decreased (longer plug at the crack tip). The figures in the following section illustrate the interaction between these plugging parameters (at the fracture tip and formation damage), with injection pressure and fracture length.
Results and Conclusions
For a fixed crack
radius, R, and selected values of the dimensionless plug length, measured by 
, the dependence of the crack pressure, pi,
on the permeability ratio, measured by y, is plotted in Figure 4. The crack pressure is seen to rise as
either the damaged zone permeability decreases or as the plug length
grows. These results make physical
sense as permeability reduction and plug length growth both cause an impediment
to fluid leakoff from the fracture into the injection zone.
Figures 4 and 5 show results for the case with no plug [(R-a)/R =0] and for different ratios of the (damaged region radius)/(crack length). These curves demonstrate that the injection pressure and the stress intensity factor (because of differing degrees of fluid lost to the formation) both increase with a reduction in the damaged zone permeability and an increase in the size of the damaged zone - as is intuitively expected.
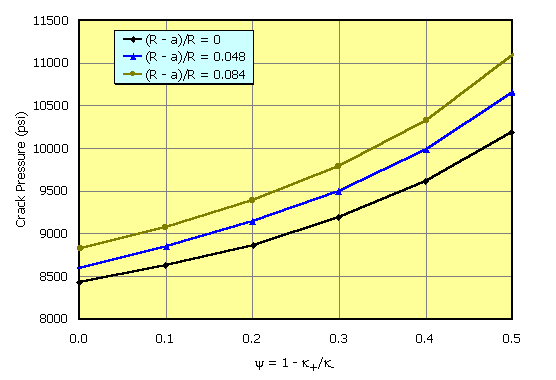
Figure 4. An example simulation of the variation in the pressure in the fracture with the magnitude of the reduction in permeability in the damaged zone. A larger value of y implies that the permeability of the damaged zone is reduced. k is equal to permeability divided by viscosity, the subscript "+" denotes the damaged zone, and the subscript "-" denotes the virgin, undamaged formation. As the reduction of permeability in the damaged zone increases, the pressure in the fracture increases. As the extent of tip plugging increases, the pressure in the fracture also increases because pressure is not transmitted to the fracture tip to allow propagation (fixed crack radius).
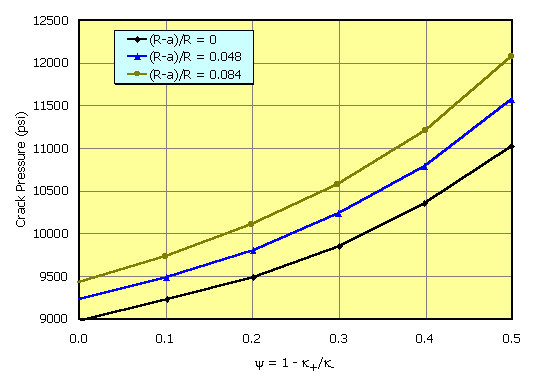
Figure 5. An example simulation of the variation in the pressure in the fracture with the magnitude of the reduction in permeability in the damaged zone. This is similar to Figure 4, with the exception that the injection rate is 43 percent higher. More precisely, the ratio of the rate to the product of k/m and R is 43 percent higher. The consequence is an increase in the fracture pressure - caused by increased rate and/or decreased damage zone permeability, and/or increased viscosity and or an increase in the overall length of the fracture. A larger value of y implies that the permeability of the damaged zone is reduced. k is equal to permeability divided by viscosity, the subscript "+" denotes the damaged zone, and the subscript "-" denotes the virgin, undamaged formation. As the reduction of permeability in the damaged zone increases, the pressure in the fracture increases. As the extent of tip plugging increases, the pressure in the fracture also increases because pressure is not transmitted to the fracture tip to allow propagation.
Figure 6 is an alternate representation, demonstrating the increase in the injection pressure with an increase in the extent of the permeability-damaged zone.
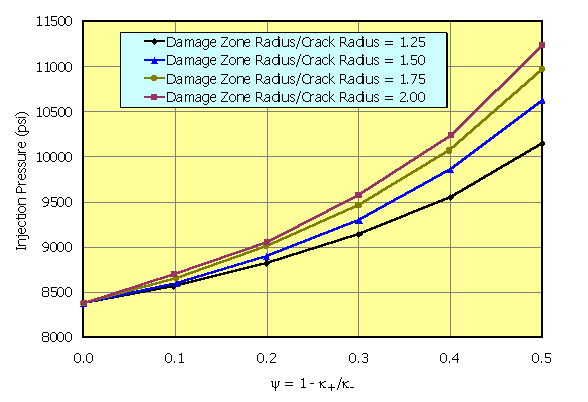
Figure 6. This is a plot of the injection pressure with the degree of damage in the formation due to fluid loss. Moving along, the abscissa, it can be seen as the permeability of the damaged zone decreases, the pressure increases. In addition, looking at the three different curves, as the extent of the damaged zone increases, the injection pressure also increases.
Field experience has shown that, to maintain a fixed injection rate, the required injection pressure changes very slowly with time (very important). It is possible that an interplay between the competing influences on KI of the damaged zone and the plug accounts for this gradual injection pressure change.
In the following example, the nature of the damaged zone - plug length interplay indicates that the fracture can maintain a steady rate of growth while both the injection pressure and the injection rate remain nominally constant as damage (measured either by the damaged zone permeability decrease or the damaged zone extent) increases. The fracture growth criterion remains constant while both the crack radius and the plug length increase.
Initially the crack has no damaged zone and no plug. In that situation, as either
d = (damaged zone
radius)/(crack radius) = 
, or,
y = 1 - (permeability ratio) = 
are increased, the values of the crack radius, R, and the plug length, R-a, are found so that the initial value of the stress intensity factor, KI, occurs while the injection rate, Q, has a value of Qo.
Consider Figure
7. In this figure, each curve is
for a fixed, but different permeability in the damaged zone. An increase in y means a reduction in the permeability in the
damaged zone. The dimensionless
damaged zone radius 
is the
abscissa, the dimensionless plug length [(R-a)/R] is the ordinate and the
parameter varied is y which is indicative of the magnitude of the
permeability reduction. For each
curve in Figure 6, initially, there is a rapid rise increase in the length of
the plugged zone at the tip with an increase in the extent of the dimensionless
damaged zone (damaged zone radius)/(crack radius). The rate at which the tip plug grows decreases with
increasing extent of the damaged zone up to a value of approximately 1.5, after
which it levels off and then the dimensionless plugged length (plug
length)/(crack radius) decreases slightly from its maximum value.
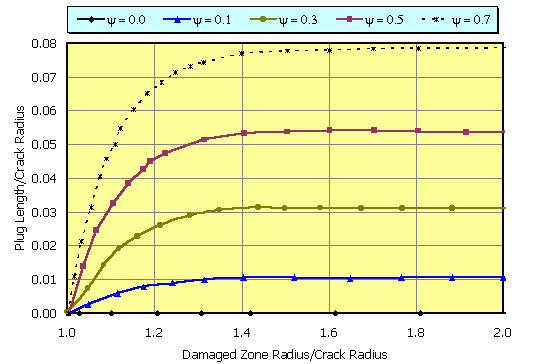
Figure 7. This is a plot of the length of the plugged zone at each tip of the fracture (non-dimensionalized by the fracture radius) with the extent of damage in the formation due to fluid loss. Moving along, the abscissa, it can be seen that as the extent of the damaged zone increases, the plug length first increases rapidly up to reach a constant plug length-to-crack radius ratio. In addition, looking at the four different curves, as the permeability of the damaged zone decreases, the plug length to crack radius ratio also increases. [supported by mass balance considerations].
Figure 8 shows how the crack radius is altered by damage. Each curve is for a constant (but different) damaged zone permeability. As the size of the damaged zone increases, the radius of the crack grows monotonically. The rate of growth of the crack radius decreases with the size of the damaged zone.
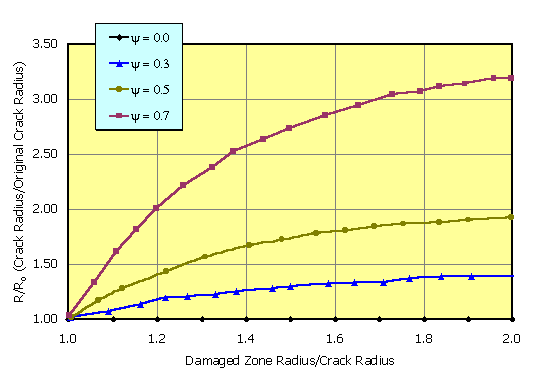
Figure 8. This is a plot of the length of the fracture (non-dimensionalized by the original fracture radius) with the extent of damage in the formation due to fluid loss. Moving along, the abscissa, it can be seen as the extent of the damaged zone decreases, the radius increases. In addition, looking at the three different curves, as the permeability of the damaged zone decreases, the crack radius also increases.
Figures 7 and 8 show the interplay between the plug length and crack radius when both the injection pressure and the injection flow rate are held constant. The figures show that a nearly constant value for (plug length)/(crack radius) is approached as damage continues to increase. The crack radius grows monotonically at a decreasing rate as damage continues to increase.
