Perkins and Gonzalez Model

 

Basic Description of the Model[1]

 

This is one of the earliest fracturing models that consider thermal stress and pore pressure change during injection.  The model considers thermal stress that would result from cooled regions with fixed thickness and elliptical cross section.  Thermoelastic stresses for a region with an elliptical cross-section and finite thickness are determined approximately with a numerical procedure.  Empirical equations were developed to estimate the average interior thermal stresses in elliptical cooled regions of any height.  Stress changes induced by pore pressure changes during fracturing are calculated using the same equations that were derived for thermal stresses.  Since for linear elasticity, the form of the equations is the same, this is accomplished by replacing the linear thermal expansion coefficient with the coefficient of pore pressure expansion and temperature change with pore pressure change.  The computed thermal stresses and stress changes due to pore pressure changes are coupled with closed-form solutions for a PKN hydraulic fracturing model to determine fracture dimensions – including length and width as functions of injection volume or time.  Examples, using typical elastic and thermal properties, showed that injection of cool water can reduce in-situ stresses around injection wells substantially, causing them to fracture at pressures considerably lower than would be expected in the absence of the themoelastic effect.  Thermal effects have been proved to be a very important factor in many water injection projects. [2]^,[3]  A mechanism is also presented in the model to study the effect of water quality on injection performance.

 

Thermoelastic Stress and Stress Change Due to Poro-Elasticity

When water is injected during PWRI, a region of cooled rock forms around the injection well.  This region grows as additional water is injected.  At any time, its outer boundary is approximately described as an ellipse that is confocal with the line crack (2D fracture).  Three zones with sharply defined boundaries are assumed (see Figure 1):

 

1.     The cooled-and-flooded ellipse from the wellbore out,

2.     Followed by a flooded, but not cooled? ellipse (the same temperature as the virgin reservoir, but increased injection water saturation) and,

3.     The undisturbed virgin reservoir.

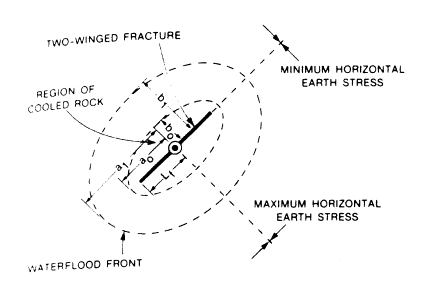
Figure 1.        Plan view showing a two-winged vertical fracture oriented perpendicular to the plane of minimum horizontal in-situ stress.

 

Thermoelastic stresses for regions of elliptical cross-section and finite thickness were determined approximately with a numerical procedures.  The following empirical equations were developed to estimate the average interior thermal stresses in elliptical cooled regions of any height:

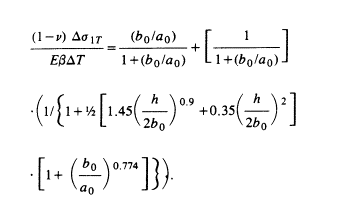
where:

 

Ds_1T ......................  thermal stress in the direction perpendicular to the fracture,

Ds_2T ................................  thermal stress in the direction parallel to the fracture, 

E .......................................................................................... Young’s modulus,

n .............................................................................................. Poisson’s ratio,

b ..................................................... linear thermal coefficient of expansion, and

h ....................................................................................... reservoir thickness.

 

If it is assumed that the porosity and permeability are independent of the stress level, the change of stress induced by pressure change can be computed in a similar manner to the change in stress that is induced by a temperature change, with the linear thermal expansion coefficient replaced by the linear coefficient of pore pressure expansion.  However, it should be noted that the equations for thermal stresses are obtained numerically with the assumption that the temperature in the elliptical region is uniform.  This may be a good assumption, based on the numerical results, if the heat transfer is dominated by convection.  Pressure in the elliptical region is not uniform and stress changes due to pore pressure changes may have to be computed from a reservoir model.

 

Size of the Injected and Cooled Regions

The injected (flooded) region is approximately elliptical in shape, in its plan view, and it is confocal with the fracture length (Figure 1).  The size of the elliptic region, its major and minor semi-axes, can be determined from volume balance of the injected water.  The cooled region is also approximated as elliptical in cross-section, and is also confocal with the fracture; the major and minor semi-axes of the cooled region are determined from an energy balance.  Heat transfer and energy loss to the upper/lower bounding layers are not considered.

 

Pressure Equations

The bottom hole pressure in the wellbore is given as:

 

where:

 

p_R ......................................... reservoir fluid pressure far from the injection well,

Dp₁ .............................. pressure rise at the elliptical boundary of the flood front,

Dp₂ ............... pressure increase between the flood front and the hot/cold front ,

Dp₃ .................... pressure increase between the hot/cold front and the fracture,

Dp_S .......................... pressure increase across skin damage at the fracture face,

............. difference between the wellbore pressure and the average pressure

                                                                          at the face of the fracture, and

Dp_p..................... pressure drop through perforations connected to the fracture.

Equations and/or descriptions on how to compute each of the above terms are given by Perkins and Gonzales (1985)¹.

 

Opening of Secondary Fractures

Because the cooled region is nearly circular in shape when the fracture length is short, the thermally-related reduction of the horizontal stresses is nearly uniform in all directions.  As the fracture length becomes large, the cooled region becomes more elongated.  As the cooled region elongates, the thermal stress reduction parallel to the fracture exceeds the thermal stress reduction perpendicular to the fracture.  This tends to reduce the difference between stresses within the cooled region and it is possible at some point the stress parallel to the fracture becomes as large as the stress perpendicular to the fracture.  When this happens, fractures may initiate along the original fracture surface and propagate in the direction perpendicular to the original fracture.  Whether this will happen or not depends on the difference in the principal horizontal stresses that are initially present in the reservoir, the thermal coefficient of expansion, the temperature change and the elastic modulus.  This process is depicted in Figure 2.

 

Example Problem

An example problem was provided by Perkins and Gonzales.  It showed a BHIP (after thermal stress reduction) that was well below the initial minimum horizontal stress.

 

Summary

1.     Thermal stresses resulting from a step change in temperature, across a region of elliptical cross-section and finite thickness are considered.

2.     Stress changes due to pore pressure changes are considered.

3.     These stress changes are coupled with the PKN model.

4.     Damage due to suspended solids is considered.

5.     An example using typical elastic and thermal properties of rocks shows that the injection of cool water can reduce earth stresses around injection wells substantially, causing them to fracture at pressures considerably lower than would be expected in the absence of the thermoelastic effect.

6.     Depending on the shape of the cooled region and the difference between the minimum and maximum in-situ horizontal earth stresses, fractures perpendicular to the main two-winged fracture could eventually open, thus creating a "jointed" fracture system.

 

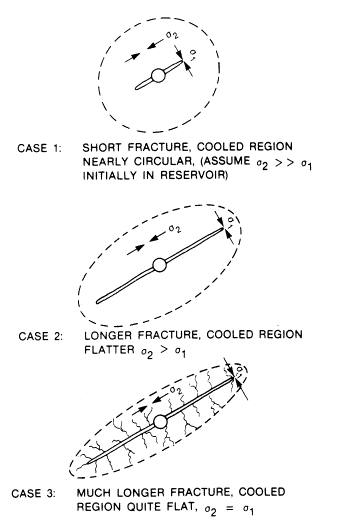
Figure 2.        Plan view showing that the shape of the cooled region controls the ration of principal stresses within the cooled region.