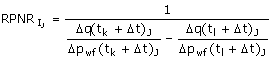Pressure Transient Evaluations in Layered Formations - CSLT (Commingled Single Layer Test)
Ehlig-Economides provided a deconvolution for transient pressure and flow rate data that reveals the single layer transient response of each zone without having to isolate the zone with packers or flowmeters. The reference is:
Ehlig-Economides, C.A.: "Model Diagnosis for Layered Reservoirs," SPE 20923, paper presented at Europec 90, The Hague, The Netherlands (October 22-24, 1990).
The Multilayer Transient Test (MLT) involves a succession of pressure and flow rate transient measurements, each above one of the reservoir zones. Each transient is induced by a change in the surface rate. For this test, each transient measurement represents the response of a multilayer reservoir that has as many layers as there were below the flowmeter during the time of the measurement. Using MLT data acquired in the standard way, the deconvolution yields a response for each zone that closely resembles the behavior that would be observed in a conventional test of the isolated zone.
When a succession of MLT measurements has been acquired above and below a zone, the near-wellbore condition, heterogeneity and outer boundaries can be identified for that zone on a log-log plot of the deconvolved data. If measurements are acquired above all flowing intervals, the multilayer reservoir model is constructed as a composite of the models and parameters estimated from each zone deconvolution.
Possible testing configurations for multilayered reservoirs are:
-
Isolate each zone with packers. This is undesirable because of the expense, time and operational effort.
-
The MLT test is conducted using a PLT with continuous monitoring of pressure and sandface rate. Pressure and rates are measured sequentially. The tool is moved.
-
The commingled single layer test (CSLT) uses a PLT with more than one flow meter.
Interpretation of MLT data is complicated by the presence of near-wellbore features, heterogeneity, or outer boundaries that are not readily identifiable on a layer by layer basis using current interpretation techniques.
An alternate testing technique using a production logging tool with more than one flow meter has been called the commingled single layer transient (CSLT) test. Logistical and calibration details have discouraged widespread application. Nevertheless, it is a concept that could be worthwhile because it can subtractively identify zone specific flow transients.
Each layer can be described by any model previously developed for single layer interpretation (i.e., Ehlig-Economides and Joseph, 1987). Mavor and Walkup described the "parallel resistance" model for commingled layers. This generalization provides a multilayer model made up of a collection of single layer models that have been formulated as solutions in Laplace space. Kucuk and Wilkinson offered a solution for the commingled multilayer model using Green's functions (this could handle different initial pressures or layers opened to flow at different times). Larsen produced solutions for zones at different initial pressures.
Some of the other highlights of this reference are as follows.
-
For isolated zone tests, selection of the model for interpretation is accomplished using a log-log plot of the pressure change and its derivative (this is, by and large, standard protocol).
-
For CSLT tests, a log-log plot of the convolution derivative is used to diagnose the model.
-
MLT test interpretation includes Selective Performance analysis, SFRC analysis above each zone, sequential analysis and simultaneous analysis - permeability, skin and average pressure for each layer.
-
Multilayer Transient Test Deconvolution. When pressure and sandface rate are simultaneously measured, the Gladfelter deconvolution or rate-normalized pressure resembles the pressure transient response to a step change in the sandface rate. For the CSLT test, flowmeters are positioned above and below the tested interval and a simple subtraction (qj(t) - qj+1(t) indicates rate to the zone. Then, a log-log plot of the convolution derivative or the deconvolution derivative is used to diagnose a reservoir model for the single layer. That is plot (in log-log coordinates):
-
If infinite acting radial flow is identified in the transient, plot the derivative of:
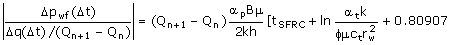
against the radial sandface rate-convoluted time function given by:
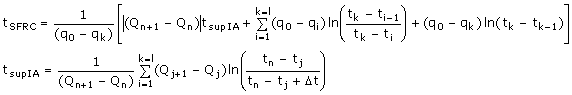
-
If the late-time behavior is not infinite acting radial flow, plot the derivative of:
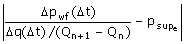
against the radial sandface rate-convoluted time function given by :
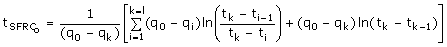
where:
| pwf .................... |
flowing bottomhole pressure, |
| t |
time, |
| q |
downhole flow rate, |
| Q |
surface flow rate, |
| n |
number of surface rate changes, |
| subscript n |
number of the current transient, |
| subscript k |
transient start time index, |
| subscript l |
transient start time index, |
| ap |
units conversion factor for dimensionless pressure, |
| B |
formation volume factor, |
| m |
fluid viscosity, |
| t>SFRC |
sandface rate convolution time function, |
| t>SFRC0 |
sandface rate convolution time function, |
| k |
permeability, |
| ap |
units conversion factor for dimensionless pressure, |
| f |
porosity, |
| ct |
total compressibility, and, |
| rw |
wellbore radius. |
-
For the MLT, it is not possible to subtract the flow rates from a transient measurement made at different times. Dividing by the simultanteoulsy measured pressure change normalizes the time-dependent flow rate change from each transient. The resultant pressure-normalized rate has been corrected for flow rate fluctuations and for the magnitude of the surface flow rate change that initiated the transient. Subtract consecutive (above and below a zone) pressure-normalized rates. "The reciprocal pressure-normalized rate difference (RPNR) is a convenient extension of the Gladfleter deconvolution. The log-log plot of the RPNR and its derivative with respect to the logarithm of time provides response patterns like those of the pressure change and its derivative."
-
For interval IJ, the RPNR is:
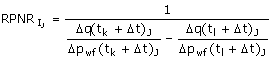
-
The derivative of the RPNR with respect to ln(Dt) is an analog to the pressure derivative for an isolated zone test. However, only early time can be used for modeling. "The rule of thumb for pressure buildup tests is that superposition effects are negligible for a length of time equal to 10 percent of the duration of the previous flow period. For flowing transients, the behavior may be significantly affected by superposition even earlier in the transient. Considerable distortion can occur very early in time."
-
Distortion is reduced in the pressure derivative response by differentiating with respect to the superposition time function, tsup.
-
If the behavior at the end of each period is IARF, the above convolution derivative accounts for superposition. If outer boundaries of heterogeneities affect the later-time behavior, the response at each level can be corrected using the desuperposition derivative.
-
"If outer boundaries for all layers are the same, then the correction determined from a representative transient for the total system [typically a representative transient response results whenever the rate is increased and the rate change is a large magnitude] can be applied to the convolution derivatives at each level. However, if an objective of the MLT test is to characterize different outer boundaries for each layer, the test may require two transients (one flowing, one shut-in or flowing at a low rate) per layer.
-
To compute the deconvolution derivative response for layer IJ the deconvolution derivative above each layer is used.
![]()
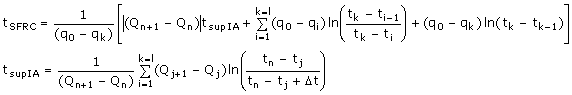
![]()
![]()