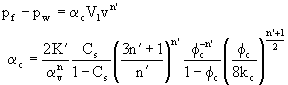Modified Hydraulic Fracturing Stimulation Simulators

With injection into higher permeability formations and increased considerations over flowback design and in-situ measurements, the stimulation community has itself made efforts to modify their simulators. van den Hoek, 2000, asserts that changes in representation of fluid loss relationships are essential for modeling fracpacking and cuttings reinjection. "In high-permeability reservoirs, leak-off rate may be high enough compared to fracture propagation rate to the extent that using the 1D Carter model ... is not justified anymore. This is especially true for those cases where the reservoir flow contribution to total leak-off is the controlling factor, as can be the case for fracpacking operations."

Settari, 1980, had shown that the classical form of fluid loss coefficient is strictly valid only when the permeability in the direction of the fracture is zero or when the leakoff rate is small. Nghiem et al., 1982, presented a fully implicit model, coupling reservoir flow, fluid loss and fracture growth for multiphase situations. Settari, 1980, had previously developed a sequentially coupled model. Fan and Economides, 1995, described relationships for pressure-dependent leakoff. Their method was based on flow of a non-Newtonian fluid in a porous medium. Plahn, et al., 1995, used a reservoir model to evaluate fracture morphology during closure. The real value of that paper may be the change in modeling philosophy where reservoir mechanics are merged with fracture mechanics.

Yi and Peden, 1994, demonstrated a model, with realistic components. They included non-Newtonian fluid flow in the invaded zone. A representation of Darcy’s law, using power law methodology, was presented. There was Newtonian fluid flow in the reservoir zone. Ahead of the filtrate, formation fluid is displaced farther into the reservoir. This described flow of filtrate (fluid that has passed through the cake). Finally, within the fracture itself, cake is developed. The pressure gradient through the filter cake is proportional to the leakoff velocity raised to the nth power. Concurrently, the filter cake grows due to deposition. If the concentration of the materials causing cake development is C_s, a pressure drop relationship could be expressed as:

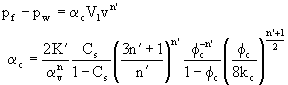    (7)

where:

p_f is the pressure at the fracture face,
p_w is the pressure behind the filter cake,
a_c is a filter cake factor,
V_l is the leakoff volume,
a_vⁿ is a conversion factor,
C_s is the concentration of pseudo-solids in the cake,
f_c is the filter cake porosity,
k_c is the filter cake permeability, and,
a'_c is the corrected cake factor accounting for erosion.

The numerical procedures are as follows.

• Solve for the pressure profiles in the invaded and the reservoir zones. Discretize with standard finite difference techniques.
• Iteratively couple this with the filter cake model in accordance to specific far-field pressure or flow boundaries.
• Knowing the pressure profiles, calculate the leakoff velocity distribution.

Mayerhofer et al., 1993, also recognized the importance of more explicitly coupling reservoir flow with fracture geometry, particularly for analyzing fracture calibration (minifrac) tests. They stated that the concept of the leakoff coefficient does not discriminate the controlling phenomena and the nature of their inherent deviations from ideality. "Fluid loss occurs normal to the fracture face through the filter cake, and into an invaded zone which does not extend more than a few centimeters into the formation. Outside the filtrate invaded zone the pressure perturbation may extend for a significant distance into the formation." These authors explicitly separated the pressure drop occurring in the reservoir and in the filter cake. "Traditionally, specific leakoff coefficients have been postulated for separate phenomena such as compressibility-controlled, viscosity-controlled etc. ... Then the individual zones have been combined as conductances in series. A simple (harmonic average) and some more complicated techniques have been used to calculate the combined leakoff coefficient. Instead [they] addresse[d] the individual pressure gradients in their correct relative contribution and the components are added as resistances in series. This approach is straight-forward, since the solutions are given by well-known filtration models, that have been used frequently in well testing applications."

Mayerhofer and Economides, 1993, presented a model which decoupled the reservoir and filter cake behavior as flow in the formation from a transient infinite-conductivity fracture with a rate and time-dependent skin effect. The assumptions made included:

• Piston like displacement of the reservoir fluid by the filtrate,
• The filtrate-invaded zone was modeled as a steady-state, but varying fracture face skin effect, added to the varying filter cake resistance.
• The analysis did not account for pressure dependence of the fracture face skin, relevant if there is significant pressure drop across the cake.
• A material balance and PKN geometry considerations characterized, leakoff during closure.

Valko et al., 1997, developed a radial flow model to represent two-dimensional reservoir flow that is associated with high permeability fracturing (for stimulation/completion).

Using a planar three-dimensional fracturing simulator, Morales et al., 1986, approximated growth of a waterflooding induced fracture, resulting from filtered seawater injection into an oil-bearing limestone reservoir. Since the injected fluid was filtered seawater, fines were probably restricted. "The fluid loss rate was assumed to be represented by classic leakoff theory by the combination of the fluid loss coefficients C_c and C_v for the reservoir fluid and the injected fluid respectively." Height growth was represented. An important observation was the rapid loss in thermal barriers to vertical growth once those barriers were ultimately penetrated by the fracture.

Clifton and Wang, 1988, summarized three-dimensional modeling concepts in TerraFrac^TM, the code used by Morales et al. - particularly fluid loss and thermal stress effects. Leakoff through the walls occurs at a rate determined by the difference between the pressure in the fracturing fluid and the remote pore pressure divided by the time elapsed since the local fracturing surface was first exposed to the fracturing fluid. The fluid loss coefficient is normalized by the difference between the minimum in-situ compressive stress and the in-situ pore pressure. "The assumed proportionality of the fluid loss rate to the pressure difference (p-p_f) is consistent with the solution for one-dimensional flow into a semi-infinite porous medium with far-field pore pressure p_f and a constant pressure p maintained at the injection plane.

van den Hoek, 2000, reviewed existing stimulation models and how fluid loss was represented. He concluded that "none of the efforts addressing non-linear fluid flow around a hydraulic fracture have resulted in a model that can be used for a fracture propagating at arbitrary but not necessarily constant, velocity, i.e., that can be used to describe the growth of a fracture that propagates through a multi-layer reservoir, with stress contrasts (leading to (temporary) retardation/acceleration of frac growth) and rock mechanical property contrasts, and that can also be used to describe the fracture closure after shut-in." A numerical solution will be presented in that paper for the fully transient elliptical fluid flow equation around a propagating hydraulic fracture for arbitrary pump rates(s). In addition, a simple analytical formula for leak-off rate is presented that is shown to yield an excellent approximation of the numerical results, both during fracture growth and after shut-in.