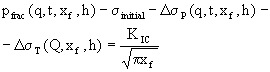Two-Dimensional Produced Water Simulators

Conventional hydraulic simulators are evolving to represent high permeability environments which are characteristic of many produced water reinjection zones. These stimulation codes do not necessarily explicitly represent the influence of fines and associated plugging, and rarely represent the poro- and thermoelastic effects adequately. The waterflooding and produced water communities have modified available codes or have developed new models to represent these effects. As with stimulation hydraulic fracturing, the first models developed were two-dimensional, either constant height or radial. Some of these models are briefly described below.

Perkins and Gonzalez, 1985, developed a model for calculating the thermo- and poroelastic stresses that are induced within elliptically shaped regions of finite thickness around a fracture. Presuming constant viscosity injection into a line crack (two-wing, constant height, vertical fracture), the flood front propagates elliptically. A region of thermal alteration, with a reasonably sharp front chases the flood front (also elliptical). They cited the thermoelastic changes in an infinitely long elliptical cross section and approximations were derived for finite thickness situations. These authors used Lubinski's developments to include poroelastic effects. Following the conventional Perkins and Kern methodology, the fracture is assumed to start and initially grow radially, after which continued growth is lateral and confined. The stresses affecting growth are impacted by thermoelastic and poroelastic stress changes. One particularly interesting concept is the potential for development of secondary fractures.

Koning's analytical model,(Koning, 1988) calculates fracture length, bottomhole injection pressure and dimensions of the waterflood front for a user-specified injection volume, V_inj. The waterflooded formation layer (with thickness, h) is bounded by impermeable zones above and below. The fracture, with a half-length, x_f, is at the centre of a set of concentric ellipses representing a zone where the reservoir temperature has changed, a flooded zone, and an unflooded virgin zone (oil zone). Each region is characterized with its own mobility. Adopting a Geertsma and deKlerk methodology, the length is determined from:

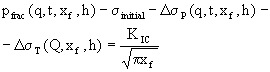    (8)

where:

p_frac is the fluid pressure in the fracture (uniform, since the fracture has infinite conductivity),
q is the injection rate,
Q = qt is the injected volume,
t is the time,
x_f is the fracture half-length,
h is the total height of layer and fracture,
s_initial is the total minimum in-situ principal stress (before injection),
Ds_P is theporoelastic back stress on the fracture face,
Ds_T is the thermoelastic back stress on the fracture face, and,
K_IC is the Mode I fracture toughness.

The pressure, p_frac, is based on a steady-state solution for a two-dimensional, infinite conductivity fracture, accounting for the individual zones with different mobilities. Using this late-time transient approximation implies that fracture propagation is very slow in comparison to the diffusion of the fluid. In situations where this is not the case (i.e., low permeability injection or stimulation) this approach is unacceptable. From this pressure profile, Koning derived an analytical expression for poroelastic effects and adopted the Perkins and Gonzalez relationships for thermal effects.

Ovens and Niko, 1996, formulated a radial version of Koning's model. They combined the Barenblatt fracture growth criterion with changes in back stress to derive a formulation relating changes in length to changes in fracture pressure. Presuming that superposition is appropriate, the state of stress near the fracture tip was determined from the summation of two stress fields. The first one relates to the deformed surface resulting from the pressure applied to the fracture. The second stress state was for a continuous body subjected to body forces, in this case the loads arising from the pore pressure or temperature fields acting within the rock. An oblate spheroidal coordinate system has been used in formulating the equations leading to the stress changes.

For internal pressure in the radial fracture, Ovens and Niko cited an unreferenced development by Abou-Sayed giving:

    (9)

where:

R is the fracture radius,
A_p is the poroelastic parameter,
p_i is the pressure in zone i,
is the far-field formation pressure, and,
is the far-field stress.

This was used in conjunction with thermo- and poroelastic stresses and volumes for a damaged zone, a cooled zone and an invaded zone. These expressions were used to evaluate an analytical version of Sneddon's relationship for a penny-shaped crack.

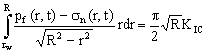    (10)

where:

p_f(r,t) is the fracture pressure,
r is the radial position,
t is the time,
s_n is the normal stress, and,
K_IC Mode I fracture toughness.

Damage was accounted for. Ovens and Niko indicated that a rigorous way to include the effect of fracture face skin or reduced conductivity was to change the pressure boundary condition that governs calculation of the state of stress associated with internal loading. Reduced fracture conductivity would alter the pressure and flux distribution over the fracture face and thus alter the poroelastic back stress. More details on this can be found in van den Hoek, 1996.

"Internal damage in the formation must be governed by the way in which the oil and solids are deposited within the formation. It is most likely that the deposition extends some distance away from the fracture face, since near the fracture the flow velocity may be sufficiently high to cause stripping of any deposited oil/solids. Thus dynamic filtration theory may be required to model this effect."

"At the present time, the new radial model only accounts for the effects of internal damage, i.e. damage extending into the formation. This damage is crudely represented by two parameters, the damage factor K_DAM and the damage volume F_DAM. The damage factor K_DAM simply scales the water relative permeability to produce an ellipsoidal zone of reduced permeability around the fracture. The volume of this zone is governed by F_DAM, which simply scales the damage volume relative to the total injected volume."

Detienne et al., 1995, presented a convenient, basic model that has worked effectively in history matching wellhead pressure and injection rates for long-term (3 to 5 years) injection. "The algorithm is sufficiently simple to be implemented in a conventional reservoir simulator." They particularly emphasized the concepts of thermally-induced fracturing (TIF). "The reservoir stress near the well is reduced when the reservoir is cooled, and fracturing will occur if the reservoir stress falls below bottom hole flowing pressure. It is this same mechanism which can sometimes be heard as you drop an ice cube into a cocktail at room temperature." TIF improves fracturing. The dimension of the cooled zone that develops around the well impacts the lengths of the fractures. The methodology adopted is as follows:

1. Wellbore Temperature Profile: A bottomhole flowing temperature is first calculated. The well is divided into segments and the transient heat exchange solution of Poettmann et al, is used.
2. Perform Calculations For Radial Injection: Matrix injection is initially assumed, bottomhole pressures are calculated and tested against the pressures required to cause hydraulic fracturing. Three radial zones are assumed - a near-wellbore cooled and flooded zone, a flooded and warmed up zone, and virgin reservoir. In each zone, pressure drop is determined. Skin is incorporated in the cooled/flooded zone. Fluid properties and permeabilities are specified for each zone. The cooled radius is calculated, the flooded radius is determined from mass balance considerations and the pressure drop is found by adding the pressure drops in the three discrete zones. Thermoelastic effects are incorporated by using the results from Perkins and Gonzalez, 1985. Elliptical cooled zones are indicated not to occur until the fracture grows beyond the radial-flow cooled zone. Poroelasticity was represented with a global effect to accommodate the evolution of the average reservoir pressure and a local effect due to pressure change in the immediate vicinity of the well.
3. Fractured Well: When the pressure becomes adequate to initiate/grow a fracture, an iterative procedure is used to find x_f. An equivalent radius is used to represent the fracture in calculating skin. The skin incorporates a fracture conductivity component which accounts for the width and permeability of the fracture, the geometric skin due to the existence of the fracture itself (s_geometry), skin that can be associated with external filter cake (s_cake), and skin associated with damage to the fracture face.

s_fracture = G + s_geometry + s_cake + s_damage

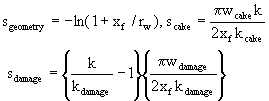    (11)

where:

s_geometry is geometric fracture skin,
s_cake is skin due to external cake,
s_damage is skin due to fracture face damage,
s_fracture is total fracture skin,
G is skin due to fracture relative conductivity, (G® 0.69, for F_CD>30),
x_f is the fracture half-length,
r_w is the wellbore radius,
w_cake is the external cake thickness,
k is the formation permeability,
k_cake is the external cake permeability,
w_damage is the depth of fracture face damage (internal cake), and
k_damage is the permeability of fracture face damaged zone (internal cake).

4. Wellhead Pressure: Bottomhole pressure is converted to surface pressure by accounting for the head and the friction.

van den Hoek et al., 1996, described a numerical model that fully couples the reservoir engineering and fracture mechanics aspects of produced water reinjection, PWRI. It incorporates finite, non-uniform fracture conductivity, fracture growth, and evolving accumulation of filter cake. The consequences of internal filter cake are addressed, as are stress changes associated with poro- and themo-elastic effects. The numerical and analytical models are appropriate for constant-height fractures which fully penetrate a permeable layer bounded by impermeable layers, although a 'square fracture' option allows a first-order estimate of radial fracture dimensions. The model is an extension of Koning's model for waterflood-induced fracturing. The fracture is surrounded by four elliptical pressure/temperature regimes. These are:

• an impaired zone where oil/solids have penetrated,
• a cooled zone (presuming the injection fluid is cooler),
• a flooded zone where the injected fluid has warmed up, and,
• a virgin hydrocarbon-bearing zone.

Each zone is characterized by its own temperature, viscosities and relative permeabilities. The extent of each zone is determined from the injected volume, the heat capacities, etc. There is an external filter cake composed of oil and solids. The internal and external filter cakes and the finite conductivity fracture were elements not included in Koning's model. For clean water injection, the propagation criterion was represented as:

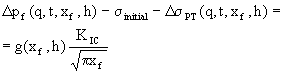    (12)

where:

Dp_f is the difference between the fracture pressure and the reservoir pressure at the start of the injection,
q is the total water injection rate,
t is time,
x_f is the fracture half-length,
h is the reservoir and fracture height,
K_IC is the Mode I fracture toughness,
s_initial is the initial total minimum in-situ stress (before injection),
Ds_PT is the sum of the poro- and thermoelastic stresses on the fracture face, and,
g(x_f,h) is a fracture geometry factor (PKN vs. KGD) [for a KGD fracture, g(x_f,h)=1].

The pore pressure profile around the fracture followed Muskat's original derivations, the poroelastic stresses followed Koning's developments and the thermoelastic stress field was determined after Perkins and Gonzalez. The damaging mechanisms were represented by:

• A damaged zone around the fracture that was characterized by a uniform "permeability impairment factor." Damage can be modification of the relative permeability in addition to solids-based damage. The outer extent of this impaired zone (internal filter cake) is calculated from the volume of injected oil and solids that deeply penetrates into the formation.
• An external filter cake with uniform permeability that accumulates on the face of the fracture. The external filter cake (forming on the face of the fracture) is assumed to have a uniform permeability. The thickness is assumed to be elliptically variable. This will provide a uniform pressure drop through the external filter cake along the length of the fracture if the fracture has infinite conductivity. Mass balance is used to determine the thickness of the external filter cake [d(x), d(0) = d₀].

    (13)

where:

d(x) is the external filter cake thickness,
d₀ external filter cake thickness at the fracture mouth,
x is the position along the fracture, and,
x_f fracture half-length.

• Once external filter cake development is initiated, it is presumed that internal filter cake development away from the fracture face will cease. Mass balance would then suggest that accumulation of solids could lead to plugging of the fracture itself and invalidation of continuing assumptions of infinite fracture conductivity, with accompanying pressure drops. The elliptical symmetry is no longer valid and pressure drop is determined semi-analytically using appropriately truncated Fourier series. Both poroelastic effects and fracture pressure depend on the position along the fracture half-length. "One problem that arises in modeling finite conductivity PWRI fractures is that both the average fracture permeability and the permeability profile in the fracture are unknown." If solids accumulate within the fracture after the initiation of an external cake (presuming dynamic stability with erosion), solids fill the fracture and flow can be concentrated into discrete channels, possibly visualized as "wormholes" within a filter cake that entirely fills the fracture. Continued injection can plug wormholes, and cause supplementary increases in local fracture width because of the consequent reduction in fracture conductivity. These authors were among the first to publicly consider two limiting cases caused by differing distributions of plugging material. These are:

1. Assuming that uniform fracture permeability will provide an upper-bound estimate of injection pressure.
2. Assuming an infinite conductivity fracture with a low permeability plug behind the tip will result in a lower-bound estimate of fracture pressure. Analytical models have been developed for this situation.

It is anticipated that the tip of the fracture will plug first and that fracture permeability will decrease towards the tip. There are two extremes that one can imagine for modeling - a uniform, but finite fracture conductivity and a tip-plugged region with infinite conductivity behind it. In the first case, iterations can be carried out on the fracture width until mass balance will allow all injected solids to be accommodated. In the latter case, it is presumed that the fracture behind the tip plug is dominantly filled but does contain adequate, discrete channels to minimize pressure drop and validate infinite conductivity assumptions, except at the tip. For the same wellhead injection pressure, case (i) [finite conductivity] will result in fractures with a smaller volume than for case (ii) [tip plugging]. On the basis of equal injected solid volumes, a lower injection pressure will characterize case (ii). "... the assumption of a uniform fracture permeability profile will lead to an upper-bound estimate of injection pressure, whereas the assumption of an impermeable plug will lead to a lower bound estimate of injection pressure."

When a uniform, finite conductivity fracture was assumed, observations from various simulations were:

• Injection water temperature has a significant impact on well injectivity.
• Determinations of filter cake permeability are problematic.
• Most simulation runs showed a gradual reduction in injectivity due to fracture plugging.
• Injectivity decreases for higher TSS, filter cake permeability, modulus, and injection water temperature,
• Fracture size increases for higher TSS, lower filter cake permeability and lower injection water temperature,
• Young's modulus had little effect on dimensions but affected pressure substantially,
• Initial injectivity is not strongly dependent on solids loading because initial growth of the fracture is relatively rapid. Initial injectivity depends on the filter cake permeability and the injection water temperature.

Where an impermeable tip plug was assumed, simulations suggested that:

• After prolonged injection, the pressures can be considerably lower than those forecasted for a uniform, finite conductivity fracture.
• Injectivity hardly decreases with time. "This seems to be more in line with BP's PWRI experience, who have been injecting for over 10 years in their Prudhoe Bay field without observing any appreciable decline in injectivity."

These authors suggested that field information might preferentially support the tip-plugging scenario, with infinite conductivity behind the tip plug. Modeling demonstrated that for a very large range of plug permeabilities, the computed wellhead pressure was fairly insensitive to the plug permeability and length (except for very high plug permeabilities). The actual mechanics of the plug are uncertain but one can speculate that the plug will be filled and compressed progressively up to a point where the wellhead pressure no longer decreases. "The above discussion suggests that the picture of a low-permeability tip plug is more realistic than the picture of a uniform fracture permeability distribution."

Analytical representation of the tip-plugging scenario is possible by using infinite conductivity assumptions over the unplugged length. In the plugged portion, the pressure profile and poroelastic stress regime are not uniform. Formulations are provided.

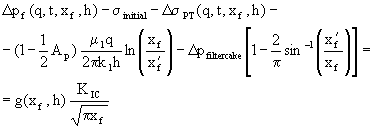    (14)

where:

Dp_f is the difference between the fracture pressure and the reservoir pressure at the start of injection,
q is the total water injection rate,
t is time,
x_f is the fracture half-length,
h is the reservoir and fracture height,
s_initial is the initial total minimum in-situ stress (before injection),
Ds_PT is the sum of the poro- and thermoelastic stresses on the fracture face,
A_p is the poroelastic constant,
m_i is the effective viscosity in zone i,
k_i is the effective permeability in zone i
x'_f is the half-length of unplugged part of the fracture,
Dp_filtercake is the pressure drop through the external filter cake,
K_IC is the Mode I fracture toughness, and,
g(x_f, h) is a fracture geometry factor.

Another significant determination by van den Hoek et al., 1996, was that the computed fracture length is quite insensitive to the degree of internal fracture plugging. This is demonstrated in Appendix B of van den Hoek et al., 1996, (Equations B7 and B13).

In 1998, Wennberg presented a description of the WID simulator that incorporates many of the plugging concepts described earlier. Current versions of the code are proprietary. Nevertheless, the philosophical methodology is as follows.

1. Determine the concentration of deposited particles as a function of distance and time. This requires us to know the initial filtration coefficient as well as the variation of the filtration coefficient with time. (find the specific deposit s). "Even more difficult to predict is the evolution of l [the filtration coefficient] as deposition proceeds." However, the formulas [discussing transition time] rely on parameters that are difficult to determine theoretically, but they can be determined by careful experiments."
2. "The next step in damage modeling is to predict how the permeability changes as a function of specific deposit (s). In general, it is difficult to relate the permeability reduction directly to the specific deposit, since the deposit morphology will have considerable impact on the permeability reduction." The deposited particle concentration must be converted to a permeability distribution ... from which the corresponding skin factor can be deduced (the version described by Wennberg used the Kozeny-Carman model). Sum the resistances in the discretization and update suspension concentration using mass balance.
3. Knowing the skin, determine the change in injectivity.

"The reliability of WID (and any other simulation effort) is dependent on a correct understanding and prediction of the deposition rate. Due to the complexity of the process, involving particle type (size, shape and mineralogy), pore space morphology, pore mineralogy, liquid type, etc., it is virtually impossible to develop a correlation that will give a correct prediction of l for all cases."