Pseudo-Three-Dimensional PWRI Fracture Simulators

As in conventional hydraulic fracturing, the next step in development of simulators has been to extend geometry with pseudo-three-dimensional considerations. Gheissary et al., 1998, extended van den Hoek's injection methodology to multi-layered reservoirs, where pseudo-three-dimensional fracture growth was represented. Previously, Koning and Ovens and Niko, 1996, had developed solutions for a contained, and a radial fracture in a vertically unbounded reservoir, respectively. Gheissary et al. presented a method that approximates the gradual transition from three-dimensional to two-dimensional elliptical symmetry, if there is no crossflow - "... a new 3-dimensional fracture growth model which permits the description of fully contained elliptical fractures within the injection layer; with the fracture length, the height upwards and the height downwards all potentially growing at different rates." "We have developed an analytical model because it needs to be coupled with a fracture simulator. A numerical model would be very time consuming as the reservoir pressure field needs to be evaluated at a large number of succeeding time steps."

Presuming slow fracture growth, change in geometry and development of the pressure field were decoupled, and the pressure field was modeled with a constant fracture length. Fracture friction was neglected (rates are low and the injected fluid is water). It was assumed that there is no vertical crossflow away from the wellbore. Close to the fracture, the pressure field was approximately that for a fracture in an unbounded reservoir, whereas farther away it is two-dimensional (asymptotically). Assuming pseudo-steady state and constant fracture pressure, analytical solutions are possible and there is a gradual transition from the three- to the two-dimensional solutions. The transition is represented by a discontinuity in the space for a fracture that is vertically centered in the layer. "The 3D-solution is taken inside the ellipsoid that touches the layer boundaries. The remainder of the reservoir is approximated by a 2D ellipsoidal volume and the associated 2D solution. A volume equal to the volume of the 3D ellipsoid is excluded, and the 2D solution beyond the 3D-2D transition is determined by an equivalent rectangular fracture over the full layer height. The boundaries of the 3D ellipsoid and the 2D excluded ellipsoid do not coincide; a pressure solution is only formulated inside the 3D ellipsoid and outside the excluded 2D elliptical cylinder. This allows pseudo-three-dimensional fracture propagation."

"In the previous 2D model, the filter cake was assumed to be uniformly distributed over the fracture wall, with a possible tip plug at the end of the fracture where no water could penetrate. However, this resulted in often very high simulated bottomhole pressures as the friction in the very narrow "sheet" of fluid would become excessive. This observation pointed us to introduce "channeling" as a mechanism to release the pressure." Channeling apparently reduces friction, reduces the area available for fluid loss, filter cake thickness is reduced, and an increased pressure may be required to obtain the same opening as with sheet flow. With more channeling, the pressure reduces and the fracture length increases. Gheissary et al. found that:

• Simulations are very sensitive to variations in oil viscosity with depth and temperature.
• Simulations are very sensitive to the variations in water relative permeability with depth.
• The simulator is unable to duplicate published field observations where there have been very rapid changes in the injection behavior when the TSS is changed.

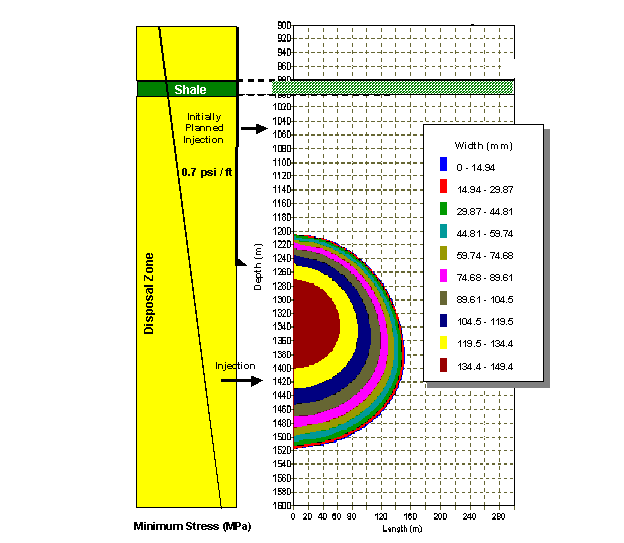
Figure 4 is an example simulation using this model for water disposal in Oman.

Figure 4. Application of Shell's in-house pseudo-three-dimensional code for modeling produced water disposal in Oman (after van den Hoek et al., 2000).