Some Definitions

Hydraulic Impedance [Z(x)] is the ratio of the oscillatory pressure (or hydraulic head) to the oscillatory flow fluctuation at a point in a hydraulic system. Remember that this technique involves sending a pulse down the string by manipulating a valve at the surface. This causes an oscillation of pressure above the steady situation that previously existed due to gradient and/or flow. There is a pressure oscillation and associated with this (possibly out of phase with it) is an oscillation in the local flow rate. The ratio of these is termed the hydraulic impedance. Note that these are the oscillatory parameters that are superimposed on the steady-state conditions (in the nomenclature of Wylie and Streeter (1982),4 they are h' and q' (as opposed to and )).

Free Oscillations result from an initial, temporary excitation, such as the sudden removal of fluid from a pressurized well by valving, or the sudden opening of a hydraulic fracture at breakdown. When the excitation is removed, the oscillations attenuate as a result of natural physical damping in the system. The frequency of free oscillations is determined by the wavespeed of the fluid, the lengths of the system elements, and the physical properties of the system boundaries. There are also forced oscillations (steady-oscillatory behavior) where all oscillations are at the frequency of the forcing function (such as pumps during hydraulic fracturing).

Pressure is determined from the oscillatory head as P = r gH. As many of the derivations here are from standard hydraulics formulations, head, with dimensions of length will be used instead of pressure. The conversion is shown above. Note that H stands for head and not just height.

Characteristic Impedance [ZC] is the hydraulic impedance that characterizes the proportionality between head and flow moving in one direction only in a conduit (rather than at a point). In an infinite, frictionless conduit, the phase difference between head and flow oscillations is either 0 or p/w, depending on whether the flow is moving in a positive or negative direction. It is:

where:

a is the wave speed in the well (m/s),
A is the cross-sectional area of wellbore (m2), and,
g is the gravitational acceleration (m/s2).

Characteristic impedance is a special case of impedance - flow moving in one direction only. Characteristic impedance describes the relationship between head and flow change, both propagating at the speed of sound, i.e., at the wave speed a, in a conduit in the absence of reflections. For a pipe that is infinitely long in the +x direction, Z(x) = h'/q' = -ZC. For a pipe that is infinitely long in the -x direction, Z(x) = h'/q' = +Z C.

Fracture Impedance [Zf] is commonly defined in terms of the resistive and capacitive hydraulic properties of the fracture. The Flow Resistance, Rf, is the pressure change corresponding to a given flow change into or out of a fracture. The storage capacity of a fracture (Cf) is the volume change in the fracture associated with a unit change in head or pressure.

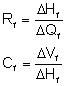
where:

Rf is the fracture resistance (s/ft2 or s/m2),
Cf is the fracture capacitance (ft2 or m2),
Hf is the change of head in the fracture (ft or m),
Qf is the change in flow into or out of the fracture (ft3/s or m3/s), and,
Vf is the change in volume of the fracture (ft3 or m3).

These act in series as a boundary condition for the momentum and mass conservation equations applicable to the oscillations in the wellbore. The resistance and capacitance of the fracture are determined by comparing measured and modeled behavior.

Holzhausen and Gooch, 1985,5 indicated the impedance of a resistive-capacitive fracture to be:

where:

i , and,
w is the angular frequency (rad/s).

Inertance (sometimes called accelerance) is associated with the inertia effects of fluid in a conduit. As a basic example, assume that the fluid is inviscid (m = 0). For a pressure drop P21 = P2 - P1 across the fluid in a conduit with an internal cross- sectional area of A, a net force P21A would accelerate the mass of fluid rAxp.(x will be used to designate length xp being pipe length and xf being fracture half-length). As a result, in a pipe:

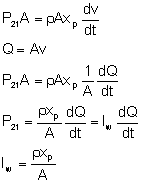
"I" is the inertance. A subscript "w' indicates that it is the inertance in the well and a subscript "f" indicates it is the response of the fracture. Some confusion can arise because many applications of inertance use a parameter that is expressed per unit length. If that is the case, consider the inertance in a well above, normalize it by the length of the pipe and express it in a relationship for head rather than pressure - giving:

Similarly, for a fracture, the inertance can be expressed as:

where:

rw is the internal radius of injection conduit (ft or m),
wf is the average fracture half-width (ft or m), and,
hf is the fracture half-height (ft or m).

Resistance recognizes the viscous effects that supplement inertial effects.

In laminar flow, following the simple example from above:

This merely demonstrates that the resistance is a parameter that interrelates the rate and the pressure drop. In the form used by Wylie and Streeter, the wellbore resistance per unit length in a pipe (for head rather than pressure) is expressed as:

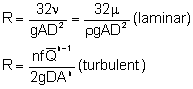
where:

n is the kinematic viscosity,
m is the dynamic viscosity,
r is the density,
D is the internal diameter,
n is the exponent for turbulent flow,
g is the gravitational acceleration,
is the average flow rate at a point, and,
f is the Darcy-Weisbach friction factor.

In laminar flow, Paige et al, 1993,2 use wellbore inertance as:

The discrepancy in these two equations needs to be resolved in this review.

The total pressure drop is a combination of inertance and resistance (in either a pipe or a fracture). It is determined as:

Capacitance: This is the storage capacity of a fluid system. For the wellbore, Wylie and Streeter use:

Paige et al, 1993 cite:

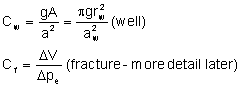
Wave Speed [a]:

The wave speed is a function of the fluid and the conduit. The basic relationship is:

where:

K is the bulk modulus of the fluid,
E is Young's modulus of the conduit,
D is the internal conduit diameter,
e is the conduit thickness, and,
c1 is the constraint parameter.

Pipe Configuration c1
Pipe supported at the upstream end only. 1.2 - n
(n is Poisson's ratio of the pipe)
Pipe anchored throughout against axial movement 1 - n2
(n is Poisson's ratio of the pipe)
Expansion joints and no change in the length of the conduit. 1
Lined circular tunnel (casing is like this)


(ER is Young's modulus of the rock)

Wave speed in a fracture is discussed later.

Reflection Coefficient [Gf]: When a wave is generated by manipulating the valve at the surface, it travels down the hole and is reflected by the hole bottom and/or a fracture opening. As Holzhausen and Gooch stated "Our goal is to derive an equation that expresses the fracture impedance in terms of the frequency and rate of decay of the free oscillations. It is a well known result from steady-state Laplace analysis that the character of free oscillations is determined by the singularities (associated with reflection) of the impedance with respect to frequency. It can be shown that:

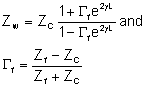
where:

g is the propagation constant (Wylie and Streeter, Chapter 7), and,
Gf is the downhole reflection coefficient.

In a limiting case, when there is no capacitance and a frictionless wellbore:

The frequency and rate of decay for a purely resistive fracture can be theoretically determined from these relationships. Similar arguments can be applied to a purely capacitive fracture, the only complicating factor being the complex terms. For additional information, refer to Holzhausen and Gooch, 1985.

<Best Practices Introduction   Click to return to HIT Introduction.
 
 
 
 
  How HIT Works> How HIT Works   The HIT concept entails interpreting the observed change in hydraulic impedance that exists between a wellbore and an open hydraulic fracture at the bottom of the wellbore.
 

Back to Key Issues Top Previous Monitoring Best Practices