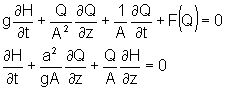
Theory
Oscillatory Flow
The momentum and mass conservation relationships must apply. These are:
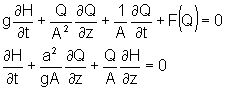
where:
H is the hydraulic head (feet or meters),
Q is the volumetric flow rate (ft3/s or m3/s),
A is the cross-sectional area of the conduit, perpendicular to the direction of flow (ft2 or m2),
g is the gravitational acceleration,
t is time (seconds),
z is distance along the conduit in the direction of flow (feet or meters), and,
F(Q) is frictional loss function depending on the conduit shape, is size, roughness and the fluid viscosity.
Inertia dominates. Diffusivity is ignored because of the time scale. In high permeability formations, diffusivity may need to be considered. The oscillations will attenuate. The time constant of free oscillation decay is:
![]()
where:
Gf is the reflection coefficient at the fracture-well junction, and,
L is the length to the junction.
"… the rate of decay becomes extremely slow as the fracture impedance approaches either zero (no fracture) or infinity (completely open fracture). Also notice that the time constant t goes to zero as the reflection coefficient goes to zero. That is, free oscillation will not occur when the fracture is open to a point where the fracture impedance and the characteristic impedance of the wellbore are equal."5
The reflection coefficient is:
![]()
where:
Zc is the characteristic impedance.
The limiting cases are Gf = 1 for Zf = ¥ (no fracture) and Gf = -1 for Zf = 0 (very large fracture).
"It therefore follows that the reflection coefficient and free-oscillation decay constant are mainly affected by the resistive component of the fracture impedance, Rf. … The effect of fracture capacitance, Cf, is mainly on the frequency content and power spectrum of the free oscillations."3 For a purely capacitive fracture:
![]()
"Thus, determination of free-oscillation frequency alone will establish the approximate capacitance of a fracture intersecting the well."5
Wellbore
The equations below are obtained from Paige et al. (1992).1 Before a HIT trace is run, the hydraulic impedance (ZW) of the wellbore can be obtained by knowing the dimensions of the wellbore and the characteristics of the wellbore fluid. As has been indicated, the governing parameters for transient flow in pipes are capacitance (CW), Inertance (IW), and Resistance (RW):
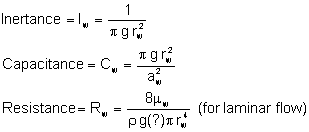
where:
g is the gravitational constant,
rw is the wellbore radius,
aw is the pulse (wave) speed in the wellbore fluid,
mw is the viscosity of wellbore fluid, and,
r is the density of wellbore fluid.
It is assumed that the resistance term is much less than the inertia term and can be ignored. Therefore, the hydraulic impedance of the wellbore (ZW) is:
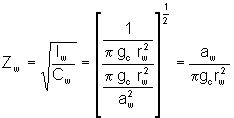
As mentioned above, a change in impedance will affect the sign of the detected signal at the wellhead, hence both a reflected and transmitted signal is created by a change in impedance. For example, a decrease in the wellbore impedance (increase in radius) will be seen in the HIT trace as an inverted reflection, and vice versa for a decrease in wellbore radius.
Fracture
The foregoing discussion conceptually demonstrates the influence of unsteady flow in a well and indicates that the properties of a fracture intersecting the wellbore impact the wave signature. The resistive and capacitive properties of the fracture can be correlated with approximations of the fracture geometry.
Assume an ellipsoidal crack in an elastic solid. The width can be expressed as:
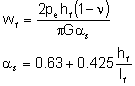
where:
pe is the excess pressure. This is the average in-fracture pressure minus the average near-fracture total stress (including poro- and thermoelastic stress changes),
wf is the fracture half-width,
hf fracture half-height
n is Poisson's ratio,
G is shear modulus (G = E/{2(1+n)}
E is Young's modulus,
as is the shape factor
("This applies to fractures with length greater than height; hf and lf should be interchanged if height exceeds length.")2,
A further description of the fracture entails determining the fracture impedance (Zf). However, the excess pressure in the fracture must be determined prior to calculating the fracture impedance. In determining the net (excess) fracture pressure, it is important to correct for the formation closure pressure; hydrostatic head in wellbore; and different frictional pressure drops in the wellbore, perforations, and near wellbore. However, before determining the fracture impedance, the fracture length can be found from the HIT trace and the excess fracture pressure by first calculating the wave-speed in the fracture (af) by:
![]()
If it is assumed that the delay in arrival time associated with the fracture (Figure 1) is the time to travel from the wellbore to the fracture tip and back to the wellbore after reflection at the tip (tf) the half-fracture length (xf) can be approximated as:
![]()
The reflection coefficient (Gf) is obtained from the measured field trace (amplitude of source pressure pulse divided by the amplitude of the reflected signal, after correcting for attenuation of signal), and the fracture impedance can be obtained from the following relationship:
![]()
where:
Zf is the hydraulic impedance of the fracture, and,
Zw is the hydraulic impedance of the well.
The fracture impedance consists of the fracture Inertance (If), and the fracture Capacitance (Cf) given below:
| Parameter | Holzhausen | Various BP Amoco Publications |
| Cf |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Cf |
|
|
|
a s |
(refer to Figure 3) |
|
| Cf (xf >> hf) |
|
|
|
Cf (xf = hf) |
|
|
|
Cf (xf << hf) |
|
|
The fundamental difference between the two formulations is the variation in the width over the dimensions of the fracture. The fracture shape factor assumes that fracture length is greater than fracture height, if the opposite is the case, hf and lf should be interchanged.
The foregoing table shows methods for estimating capacitance, depending on the assumptions made about the width distribution in the fracture. Other relevant parameters include the inertance and the resistance. The inertance is:
![]()
If resistance is ignored, the hydraulic impedance of the fracture is:
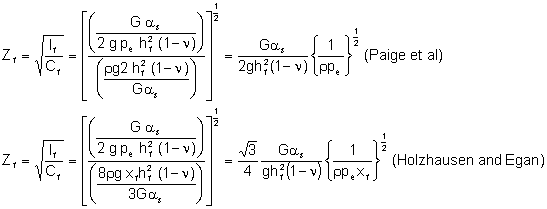
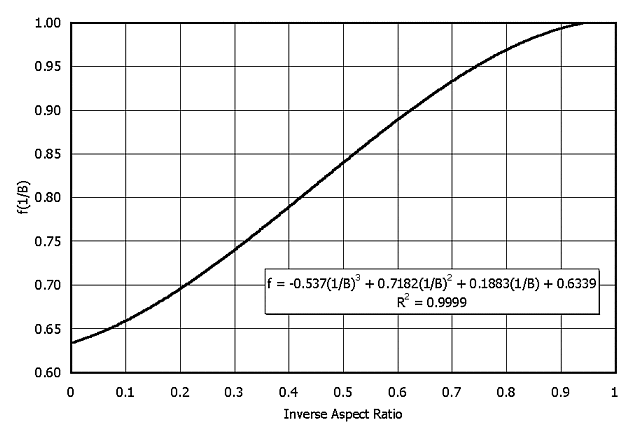
Figure 3. Function f(1/B), where B is fracture length-to-height ratio.
The fracture resistance (Rf) is the proportionality constant relating a change of flow into or out of the fracture to the corresponding change in hydrostatic head.
![]()
The fracture height is then determined from the relationship:
![]()
It is assumed that the fractures are ellipsoidal, and the fracture width (bf) is determined by the crack model given by Sneddon:
![]()
| <How HIT Works | Operational Techniques> |
|
|
|
|
|