How Can You Be Fooled?

The signature on the pressure-rate curve can be anomalous if there are reservoir variations or mechanical failure occurs during the testing. For example:

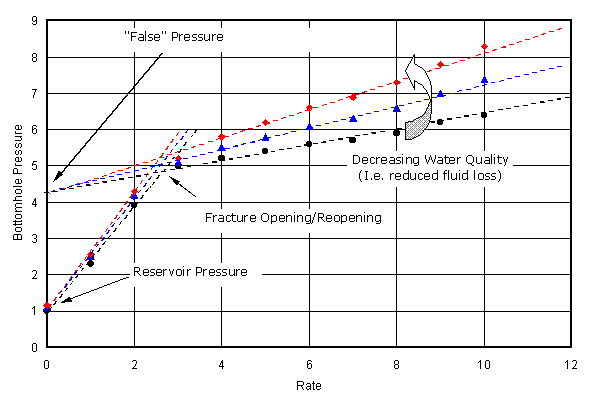
Different fluid loss. If the fracture grows out of zone into a different fluid loss regime, the slope of the post fracturing curve can vary and may not be constant. If step rate data from different tests are being compared, recognize that the slopes can be different if the water quality is different. This is shown in Figure 2. Some people only show the fracturing behavior changing (not behavior during radial flow - matrix injection). Strictly, this is not true. Slight changes can also be seen in the portion of the curve before fracture opening/reopening. Recognize that slope changes can be associated with different fluid characteristics.

Figure 2.  A schematic variation (conceptual data) of how pressure signatures can vary for different water qualities (after Murray). The slopes, after fracturing occurs, are dependent on the fluid loss. With decreasing water quality, there is reduced fluid loss, but there is additional fracture growth.

Different fracture geometry. As a note of caution, this behavior is contingent on a fracture that is contained within one zone. Much more complex behavior can occur if out-of-zone growth occurs. If the fracture grows out-of-zone dramatically, the excess pressure may decrease because of the growth more than the change in pressure due to friction in the fracture. A negative slope may appear in the post-fracturing regime. This is illustrated schematically in Figure 3. The negative slope can be related to growth into a higher permeability zone, rapid out-of-zone growth, etc. Eventually, depending on the degree of particle plugging at the tip and on the surface of the fracture, the post-fracturing slope may change strictly due to changes in efficiency.

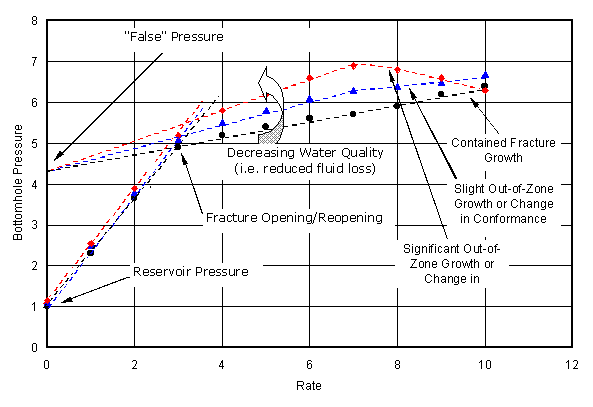
Figure 3.  A schematic (conceptual data) indicating how pressure and rate may be affected by out-of-zone growth.

Possibly different perforation friction and completion efficiency. If at all possible, bottomhole pressures should be used. For example, in a layered situation, one zone may fracture and the conformance can be changed completely. Or, the pressure drop through the perforations may be different than what you have anticipated.

Damaged cement bond. The inflection point can indicate failure of the cement sheath. It has been speculated that it may be possible to diagnose this if rates are reduced during the test (step-down after the highest rate of injection). Injectivity will apparently remain high (along the second slope) even at rates below the original inflection point. The argument against this philosophy is that if the original perforations covered the entire height, there should not be additional injectivity once a fracture closes. If the test was through a partial set of perforations, the stepdown should be on a slope that corresponds to a new kh. Considering these arguments, another reason for the increased injectivity below the original inflection point (during stepdown - reduction in rate) may be residual fracture conductivity.

Falloff behavior. It may be a toss up between doing a stepdown and a falloff test. Falloff could be important. It is very often dominated by the reservoir (short fracture closure time and gives data about stress-dependent permeability and residual permeability enhancement.

A good compromise, if possible, may be to combine both techniques - step up in rates, followed by a step down cycle (the step-down procedure may provide indications of whether or not there has been fracture growth out-of-zone, etc.), followed by stepping back up and a falloff. This may be the premium procedure and modifications may be required because of operational constraints and available time.

Packer bypass. Determining the potential for exceeding the differential pressure limits of isolation devices (if any) depends on the configuration. It may be possible to monitor backside pressure or have a bomb below the lower packer (if used in a straddle configuration).

Open pre-existing fracture. Ideally, the pressure time plot for a step-rate test would look like that shown in Figure 4. However, if there is a pre-existing fracture, it will always have conductivity, even at pressures below the reopening pressure. This is particularly true if it is self-propped (jammed open) or if we are testing a converted production well that has been conventionally stimulated. Under these circumstances, inflection may not be seen or there may be a slight curvature followed by a straight line linear or bilinear flow regime. To detect linear and bilinear flow regimes, log-log pressure-time plotting may be helpful. Examples of behavior for a pre-existing, closed and a pre-existing, self-propped fracture are shown in Figures 5 and 6.

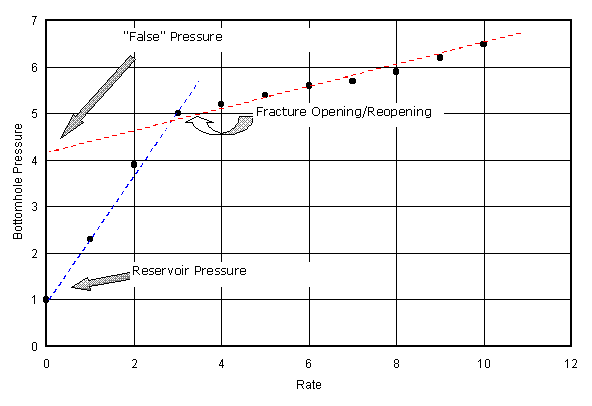
Figure 4.  An idealized, readily-interpretable step-rate test. This is conceptual data.

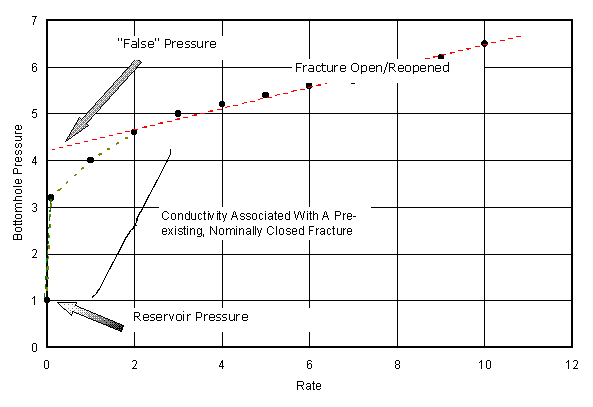
Figure 5.  An idealization of a closed (but still conductive) pre-existing hydraulic fracture.

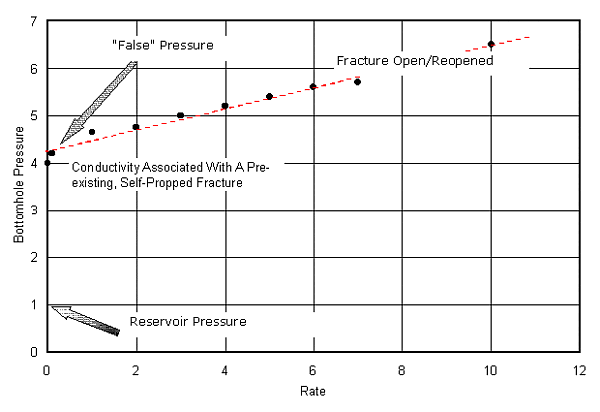
Figure 6.  An idealization (conceptual data) of a self-propped, pre-existing hydraulic fracture.

Settari and Warren (Eurorock, 1994) schematically summarized the influence of a pre-existing fracture (or at the opposite extreme, positive skin) on the step rate test signature. This is shown in Figure 7.

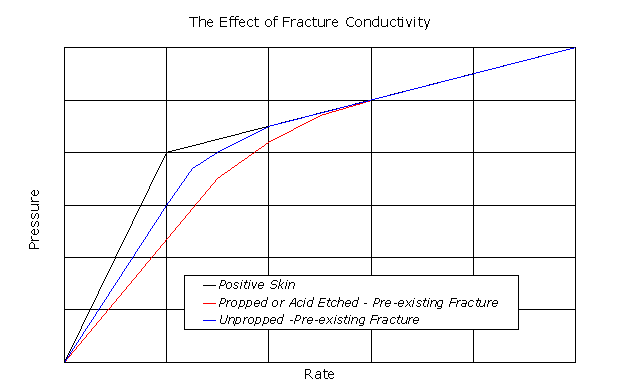
Figure 7.  An idealization of the influence of fracture conductivity on step rate test signatures (presuming propped, unpropped and damaged fractures).

Transient Effects. Depending on the volumes injected, thermal effects can come into play, either due to viscosity changes or in-situ stress changes. In conjunction with this, it is extremely important to incorporate any changes in reservoir pressure if you are comparing SRT data taken at different times in the injection life cycle.

Different Stress Levels. In comparing consecutive step-rate test programs, be certain that you are aware of any stress field alterations that have occurred due to poroelastic and/or thermoelastic effects. Measured differences can in fact be diagnostic of the stress changes associated with temperature fluctuations. Figure 8 is an example. It is not a step rate test per se. Rather it is a compilation of rate versus injection data for an actual field situation.

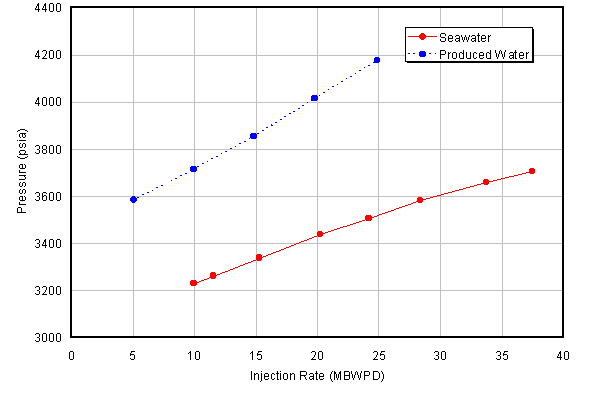
Figure 8.   This figure shows step rates for North Sea well. The PW points lie on a steeper line than the SW points. If water quality effects were small then mobility effects would be expected to make the PW line shallower. A Prudhoe Bay performance plot shows the reverse trend to this. It therefore appears that the high oil and solids content in Forties PW reduces injectivity dramatically. The effect appears to be larger than in Prudhoe Bay and this may be the result of higher contaminant concentrations and larger particle sizes.

Martins et al., 1994, discussed thermoelastic effects at Prudhoe Bay:

"The pressure required to open an induced fracture depends both on the initial stresses in the rock and on stress changes induced by injection at different temperature and pressure. It has been known since early step-rate tests that produced water has a higher fracture gradient (0.57 - 0.60 psi/ft) than seawater (0.53 - 0.54 psi/ft) [gradient values are for Prudhoe Bay]. This was linked to the higher well-head temperature of produced water (150°F versus 80°F). Most Prudhoe Bay injectors have alternated periods of seawater and produced water injection over the subsequent 10 years. It is found almost without exception that injectivity is poorer for produced water than for seawater, typically by 30-50%."

"[Injection data for Well H-09I are available on a day-to-day basis.] The well has switched 6 times between SWI and PWRI over a 7 year period. The points corresponding to SWI lie approximately on a straight line which intersects the pressure axis at about 100 psi WHP. The intersection of the straight line with the pressure axis is a good measure of the fracture-opening pressure, since step-rate tests indicate very low rates (typically less than 1000 bbl/day) beneath fracture pressure. The points corresponding to produced water injection lie on a different straight line, intersecting the pressure axis at about 900 psi. Produced water typically requires 500 psi greater pressure than seawater, in order to inject at the same rate."

"These general features are reflected in data collected from across the field. There are variations of up to a few hundred psi in the values of fracture pressure (and substantial variations in rate, depending on permeability, intervals of perforation and other factors), but the comparison between seawater and produced water follows a common pattern."

"The factors which can cause a difference in performance are water temperature (70°F warmer for produced water), viscosity (about a factor of 2 lower for produced water, which would therefore double the rate if all other factors were equal) and water quality. The dominant factor we believe to be temperature, because of thermoelastic stress. It appears that fractures are often likely to be shorter in length for produced water injection, in spite of the higher pressure."

There is a substantial amount of other data available that indicates the influence of temperature on the injection pressure. One particularly good example is from the Eider pilot program (Figures 9 and 10). Figure 9 raises certain unanswered issues. These include is there a methodology for fitting both sections of the curve. If measurements are accurately performed, the value of each point is significant and reflects specific occurrences in the reservoir. If friction is reliably considered, the curves should be forced through the origin on a plot of this nature where the y-axis is the bottomhole pressure (measured in this case) minus the reservoir pressure. This is one of the difficulties of the plot shown in Figure 1. Ideally, pressure differential plots should pass through the origin if the reservoir pressure and friction are known appropriately.

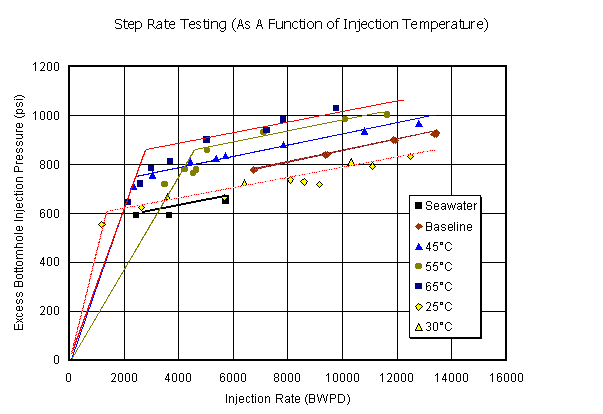
Figure 9.   These data, from a well-controlled and monitored pilot in the Shell Eider field, show the variation of measured stress levels with temperature. The lines are all approximately parallel, indicating consistency in the quality of the injected water (or insensitivity). The inferred local in-situ total stresses, as a function of temperature, are shown in Figure 10.

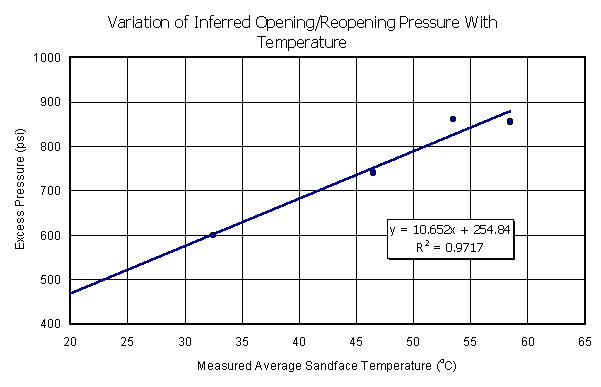
Figure 10.  Excess pressure at the inflection for each temperature regime shown in Figure 9. This clearly shows the thermoelastic elevation in the local total in-situ stress as a function of temperature.

For more information on changes in stress due to thermal and pore pressure changes:

Finally, Figure 11 demonstrates that the concepts of step rate testing can be used for evaluating long-term injection data (day by day plots of pressure versus rate) to evaluate changes in stress levels and conformance.

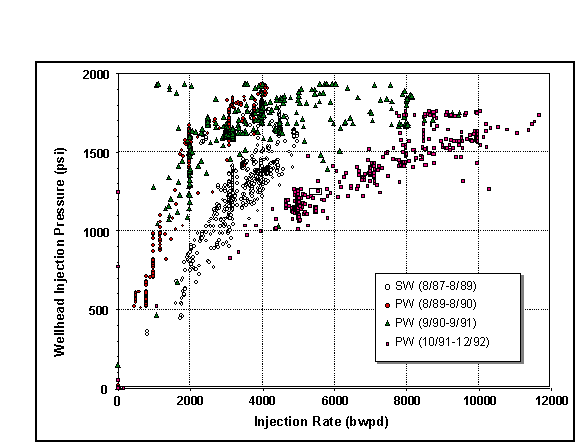
Figure 11.  Long-term variation of wellhead pressure and injection rate, showing the influence of temperature and quality. These are actual field data.

Back to Key Issues

Top

Previous

Monitoring Best Practices