Coupled Reservoir Modeling

As is evident, it is desirable to incorporate the fracture modeling with detailed reservoir simulation. This has been done at varying levels of sophistication. Ali et al, 1991, described injection above parting pressure in the soft chalk of the Valhall field. Four different simulation models were used for evaluation purposes. The first model was used to investigate the effect of injection water temperature on sweep and injectivity and to predict performance for three different reservoir descriptions. This three-dimensional, three-phase, dual porosity model (with thermal capabilities) used an effective wellbore radius approach to model the induced fracture. A second model was used to evaluate the impact of long fracture lengths and different fracture orientations on breakthrough performance. "This was a very rigorous simulation of the actual fracture, assuming a single porosity reservoir system. An in-house implicit formulation of the black oil model was used." A third model was used to address the uncertainties of fracturing. It was a single layer gridded system with three producers and one injector (dual porosity). Fractures of different lengths (all infinite conductivity) were incorporated. A fourth model was run to evaluate thermo-poroelastic effects.

"An in-house analytical fracture simulator was used to predict the thermo-poro-elastic effect ... This model assumed uniform thickness and an infinite reservoir with a propagating Perkins-Kern type fracture. It accounted for the effects of relative permeability and different viscosities for oil and water at reservoir temperature and injection temperature. The impact of fracture face plugging by solids and fracture extension as a result of injection of "dirty" water is also evaluated. The model assumes that the injected water displaces the oil in piston-like manner creating a flooded domain which is an elliptic cylinder confocal to the fracture length."

Settari and Warren, 1994, stated that "A typical waterflood pilot injection well may experience low rate water injection, below fracturing pressure, step rate tests (SRTs), several high rate tests followed by falloffs and an extended high rate injection until breakthrough is achieved>. Ideally, the model should match the entire sequence of events in order to have confidence in the predicted fracture geometry."

They recommended:

• Matching the injection below fracture pressure to provide basic reservoir characteristics and to indicate "ambient" conditions.
• Analysis of SRTs or high rate injection tests to give permeability and opening/closure pressures. Matching falloffs can give information on fracture volume, and leakoff.
• Long-term injection can provide information on stress changes in the reservoir, as can repeated SRTs.

These authors described the use of a partially coupled model and its application to both static (propped or acidized) or dynamic (waterflood) fractures. A crucial component is the representation of leakoff. Two methods were proposed:

• "Parametric" leakoff model. This assumes one-dimensional, piston-like displacement and describes the invaded (waterflooded) region by average mobility, saturation, compressibility and temperature. The leakoff model can approximate the influence of other wells or boundaries and correct the leakoff for 2-dimensional flow.
• In the numerical leak-off model, one-dimensional finite difference solutions are used for two-phase flow, heat transfer and stresses (approximately).
• With either model, each fracturing event is modeled independently and is then "interfaced" to a reservoir model at the appropriate time."

There are two evaluation components; waterflood fracturing simulation and reservoir simulation. For the fracture representation, a one-dimensional leakoff assumption underestimates leakoff. In 1980, Settari,> described a correction factor for the one-dimensional leakoff velocity as a function of a dimensionless injection rate (Q_D = Q_iw/(hC²).

    (15)

Koning, 1988, provided analytical relationships between half-length and rate, from which Settari and Warren derived relationships for the growth reduction factor, in single or multi-layered reservoir situations. For a single layer, two classical limiting cases were presented. For a large dimensionless injection rate (high rate and/or small height and/or small fluid loss):

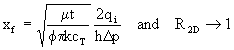    (16)

For a small dimensionless injection rate (low rate and/or large height and/or large fluid loss):

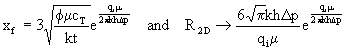    (17)

There is a significant increase in fluid loss for a small dimensionless injection rate.

A standard reference for this subject is the publication by Clifford et al., 1990. "The injection of cool surface water into higher temperature reservoirs frequently leads to thermal fracturing of the injection well. The fracture becomes a major influence on injectivity and, in some cases, on sweep efficiency. Fracture growth is dominated by stress changes due to cooling, and differs in a number of ways from the conventional hydraulic fracturing process." These authors presented results of thermal fracturing in three-dimensional reservoir structures with spatially-variable permeability. A finite difference reservoir simulator was coupled with a three-dimensional boundary integral fracture mechanics calculation. It was shown that:

• Thermal fractures could often occur in high permeability layers that cool more rapidly.
• Vertical fracture growth was found to depend on rates, pressures, temperatures, the perforation interval and on the horizontal and vertical permeability distribution.
• Most water injection wells in deep reservoirs are fractured.

"Simulation of thermally induced waterflood fracturing requires the coupling of fluid and heat flow in the fractured reservoir with thermo- and poro-elastic stress and fracture mechanics. If the fracture can be approximated as 2-dimensional, extending over the full vertical interval of the pay zone for its full length, then simple plane strain formulae may be used to describe the fracture mechanics for a linear elastic medium. Perkins and Gonzalez constructed a simplified analytic model of 2-dimensional thermally induced fracturing based on the assumption of elliptical flow fields around the fracture. Models which couple two-dimensional fracture models into a reservoir grid have been developed both for hydraulic fractures and for waterflood-induced fracturing. The Dikken and Niko model calculates the thermo- and poro-elastic stresses from the Goodier displacement potential, using methods developed by Koning."

The assumption of large vertical extent is often inappropriate and variable formation properties and layering need to be represented. The elastic modulus is the most important factor in determining thermal stress effects, in conjunction with permeability. The simulator uses a three-dimensional simulator developed by Gu and Yew, 1988, in combination with the fluid and heat flow calculation from a three-dimensional reservoir simulator. The stresses are calculated following Koning's methodology. "For a consolidated rock without a network of natural joints, it is a reasonable approximation to separate the fluid and rock mechanics elements of the problem, at each time step. The assumption is that rock porosity and permeability are nearly independent of fluid pressure and rock stress."

"It is rare for assumptions such as one-dimensional, transient leakoff, which is standard in many hydraulic fracture simulations, to be valid at any stage in thermal fracture studies. It is likely that flow over a wide region of the reservoir, including neighboring wells, will influence and be influenced by fracture growth. A reservoir simulator is therefore an essential component of the model."

"At each time step, a pressure calculation must be performed which incorporates flow both in the reservoir and the fracture. ... Options exist for treating the fracture either as having infinite conductivity or having a finite conductivity, determined by the local fracture width."

"The waterflood fracture is assumed to advance through a series of quasi-equilibrium states ... in which the stress intensity factor K_I at every point on the fracture boundary is equal to a critical value K_IC..."

Clifford et al., showed two simulation examples that are informative. The first was for a layered reservoir with moderate vertical permeability. These are communicating sandstone layers of different permeability (refer to Table 2). There is high permeability in the upper part. "Early breakthrough has occurred in production wells in the Brent formation, and has been attributed to channeling of water through the high permeability streaks in the Etive, leaving the Rannoch sands poorly swept. In order to reduce the vertical sweep problem both injection and production wells have sometimes been perforated only in the Rannoch sands."

Case 1 is perforated only in Layers 5 through 7 and a fracture initiates in Layer 5. There is substantial vertical flow into the Etive even before fracturing occurs. The fracture grows into the Etive within 20 days. Once the fracture has penetrated the Etive that zone takes most of the water and the perforation placement has not done any good. Case 2 has perforations extending into the Etive. The fracture is assumed to initiate in Layers 3 and 4. There is no growth beyond the Etive. This is advantageous because of the high stresses in the upper Rannoch. There is more cooling in the Etive.

Table 2.   Vertical and Horizontal Permeabilities

Layer	Name	Thickness (feet)	Horizontal Permeability (md)	Vertical Permeability (md)
1	Ness	57.7	1497	899
2	Ness	60.2	652	391
3	Etive	68.5	1397	1076
4	Etive	47.0	1807	1391
5	Rannoch	90.8	346	246
6	Rannoch	60.2	208	131
7	Rannoch	46.7	33	16

The second example was an artificial case; a layered reservoir with low vertical permeability (refer to Table 3).

It is undesirable to inject directly into the high permeability zone, since there would be poor waterflood performance. The desired rates cannot be achieved by only injecting into the lower permeability zones. "A realistic strategy for vertical fracture confinement must therefore include a non-perforated low permeability buffer zone between the perforated interval and the high permeability layers."

"It is therefore necessary to start injecting at relatively low rates, with a bottomhole pressure just greater than the cooled region stress. The rate is then allowed to build up gradually at roughly constant pressure, as the extent of cooling in layer 2 increases, and the fracture advances into it. The fracture must follow rather than lead the cool front."

Table 3.   Vertical and Horizontal Permeabilities

Layer	Thickness (feet)	Horizontal Permeability (md)	Vertical Permeability (md)
1	36.7	2.7	.0027
2	23.3	98.7	.0987
3	22.6	106.2	0.1062
4	15.4	39.0	.0780
5	20.7	850.2	2.5506
6	54.1	452.9	4.529
7	56.8	3.5	0.0105

"More recently, the BPOPE code has been developed, amongst other things, to allow multiple thermal fracture generation and propagation in horizontal or multi-lateral wells to be modeled. Following on from these developments our attention has now turned to the way we handle bottomhole temperature in the BPOPE simulator, given the importance of temperature on the correct prediction of thermal fractures. Typically bottomhole temperature is treated as a single, time independent parameter by many reservoir simulators." Wellbore and reservoir simulators have been coupled together. The wellbore simulator was expanded to allow multiple entry points.

Pseudo-3D Simulators

Top

Previous

Main

Documents